Coordinate Geometry - Math
Card 0 of 4973
Which of the following points would be in Quadrant III on the coordinate plane?
Which of the following points would be in Quadrant III on the coordinate plane?
Tap to see back →
Quadrant III comprises the points whose  - and
- and  - coordinates are both negative. This makes
- coordinates are both negative. This makes  the correct choice.
the correct choice.
Quadrant III comprises the points whose 


The points  and
and  are plotted on a quadrant. Which graph depicts the correct points?
are plotted on a quadrant. Which graph depicts the correct points?
The points 

Tap to see back →
A quadrant is set up in such a way that the positive numbers are to the right and top, while the negative numbers are to the left and bottom. The x-value (the first number in the ordered pair) is the distance left or right from the center. The y-value (the second number in the ordered pair) is the distance above or below the axis.
 will be
will be  units to the right, and
units to the right, and  units up.
units up.
 will be
will be  units to the left, and
units to the left, and  units up.
units up.
A quadrant is set up in such a way that the positive numbers are to the right and top, while the negative numbers are to the left and bottom. The x-value (the first number in the ordered pair) is the distance left or right from the center. The y-value (the second number in the ordered pair) is the distance above or below the axis.






Which of the followiing quadrants would contain the point  ?
?
Which of the followiing quadrants would contain the point 
Tap to see back →
 has 0 as its
has 0 as its  -cordinate and is therefore on the
-cordinate and is therefore on the  -axis, which is not part of any of the four quadrants.
-axis, which is not part of any of the four quadrants.



Which of the following points is in Quadrant IV on the coordinate plane?
Which of the following points is in Quadrant IV on the coordinate plane?
Tap to see back →
Quadrant IV consists of the points with positive 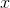 -coordinates and negative
-coordinates and negative  -coordinates. Therefore
-coordinates. Therefore  is the correct choice.
is the correct choice.
Quadrant IV consists of the points with positive 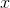


Which of the following quadrants would contain the point  ?
?
Which of the following quadrants would contain the point 
Tap to see back →
 has 0 as its
has 0 as its  -coordinate and is therefore on the
-coordinate and is therefore on the  -axis, which is not part of any of the four quadrants.
-axis, which is not part of any of the four quadrants.



Which of the following ordered pairs is in the third quadrant?
Which of the following ordered pairs is in the third quadrant?
Tap to see back →
The third quadrant is the lower left quadrant, where both the  and
and  values are negative. The point
values are negative. The point  is the only point that is in this quadrant.
is the only point that is in this quadrant.
The third quadrant is the lower left quadrant, where both the 



Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move right
, start at the origin and move right  unit and up
unit and up  units.
units.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move right
, start at the origin and move right  units and down
units and down  units.
units.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move left
, start at the origin and move left  unit and down
unit and down  unit.
unit.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move right
, start at the origin and move right  units and up
units and up  units.
units.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move left
, start at the origin and move left  units, then up
units, then up  units.
units.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
in order to get to the point  , move right
, move right  units and up
units and up  units.
units.
This is point  .
.
in order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
in order to get to the point  , start at the origin and move right
, start at the origin and move right  units and up
units and up  units.
units.
This is point  .
.
in order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to th point  , start at the origin and move left
, start at the origin and move left  units and up
units and up  unit.
unit.
This is point  .
.
In order to get to th point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to point  , start at the origin and move left
, start at the origin and move left  unit and down
unit and down  units.
units.
This is point  .
.
In order to get to point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
in order to get to the point  , start at the origin and move right
, start at the origin and move right  units and up
units and up  units.
units.
This is point  .
.
in order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
In order to get to the point  , start at the origin and move left
, start at the origin and move left  units and up
units and up  units.
units.
This is point  .
.
In order to get to the point 


This is point 

Find the point that corresponds to the following ordered pair:


Find the point that corresponds to the following ordered pair:
Tap to see back →
in order to get to the point  , start at the origin and move down
, start at the origin and move down  units.
units.
This is point  .
.
in order to get to the point 

This is point 
Which ordered pair is plotted on the following graph

Which ordered pair is plotted on the following graph
Tap to see back →
An ordered pair can be looked at like this:
(x-coordinate, y-coordinate)
where the first number represents the x-coordinate and the second number represent the y-coordinate.
The x-coordinate is simply the position on the x-axis. The y-coordinate is the position on the y-axis.
If we look at a coordinate plane, we can see where the x- and the y-axes are located.

The x-axis is horizontal (going left to right) and the y-axis is vertical (going up and down).
Now, when we graph the ordered pair  , we locate
, we locate  on the x-axis.
on the x-axis.

In this example, the y-coordinate is  . From the current position, we locate
. From the current position, we locate  on the y-axis.
on the y-axis.

This is where we plot the point  .
.

An ordered pair can be looked at like this:
(x-coordinate, y-coordinate)
where the first number represents the x-coordinate and the second number represent the y-coordinate.
The x-coordinate is simply the position on the x-axis. The y-coordinate is the position on the y-axis.
If we look at a coordinate plane, we can see where the x- and the y-axes are located.
The x-axis is horizontal (going left to right) and the y-axis is vertical (going up and down).
Now, when we graph the ordered pair 

In this example, the y-coordinate is 

This is where we plot the point 
Find a line perpendicular to the line with the equation:

Find a line perpendicular to the line with the equation:
Tap to see back →
Lines can be written in the slope-intercept format:

In this format,  equals the line's slope and
equals the line's slope and  represents where the line intercepts the y-axis.
represents where the line intercepts the y-axis.
In the given equation:

Perpendicular lines have slopes that are negative reciprocals of each other.
First, we need to find its reciprocal.

Second, we need to rewrite it with the opposite sign.

Only one of the choices has a slope of  .
.

Lines can be written in the slope-intercept format:
In this format, 

In the given equation:
Perpendicular lines have slopes that are negative reciprocals of each other.
First, we need to find its reciprocal.
Second, we need to rewrite it with the opposite sign.
Only one of the choices has a slope of 
