Matrix Calculus - Linear Algebra
Card 0 of 312
Tap to see back →
Tap to see back →
Tap to see back →
Tap to see back →
True or False, the Constrained Extremum Theorem only applies to skew-symmetric matrices.
True or False, the Constrained Extremum Theorem only applies to skew-symmetric matrices.
Tap to see back →
It only applies to symmetric matrices, not skew-symmetric ones. The Constrained Extremum Theorem concerns the maximum and minimum values of the quadratic form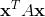 
when 
.
It only applies to symmetric matrices, not skew-symmetric ones. The Constrained Extremum Theorem concerns the maximum and minimum values of the quadratic form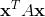
The maximum value of a quadratic form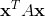 
(
is an 
symmetric matrix, 
) corresponds to which eigenvalue of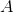 
?
The maximum value of a quadratic form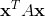
Tap to see back →
This is the statement of the Constrained Extremum Theorem. Likewise, the minimum value of the quadratic form corresponds to the smallest eigenvalue of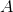 
.
This is the statement of the Constrained Extremum Theorem. Likewise, the minimum value of the quadratic form corresponds to the smallest eigenvalue of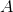
Tap to see back →
Tap to see back →
Tap to see back →
Tap to see back →
Give the Hessian matrix of the function 
.
Give the Hessian matrix of the function
Tap to see back →
The Hessian matrix of a function 
is the matrix of partial second derivatives:
.
Find the partial derivatives as follows:
The Hessian matrix is
,
or
.
The Hessian matrix of a function
Find the partial derivatives as follows:
The Hessian matrix is
or
Tap to see back →
Tap to see back →
Tap to see back →
Tap to see back →
Tap to see back →
Tap to see back →
Which of the following expressions is one for the gradient of the determinant of an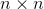 
matrix 
?
Which of the following expressions is one for the gradient of the determinant of an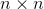
Tap to see back →
The expression for the determinant of 
using co-factor expansion (along any row) is
In order to find the gradient of the determinant, we take the partial derivative of the determinant expression with respect to some entry 
in our matrix, yielding 
.
The expression for the determinant of
In order to find the gradient of the determinant, we take the partial derivative of the determinant expression with respect to some entry
Let 
, and 
, find the least squares solution for a linear line.
Let
Tap to see back →
The equation for least squares solution for a linear fit looks as follows.
Recall the formula for method of least squares.
Remember when setting up the A matrix, that we have to fill one column full of ones.
To make things simpler, lets make 
, and 
Now we need to solve for the inverse, we can do this simply by doing the following. We flip the sign on the off diagonal, and change the spots on the main diagonal, then we multiply by 
.
The equation for least squares solution for a linear fit looks as follows.
Recall the formula for method of least squares.
Remember when setting up the A matrix, that we have to fill one column full of ones.
To make things simpler, lets make
Now we need to solve for the inverse, we can do this simply by doing the following. We flip the sign on the off diagonal, and change the spots on the main diagonal, then we multiply by
Tap to see back →
