Right Triangles - ISEE Upper Level Quantitative Reasoning
Card 0 of 136
Which of the following is true about a triangle with two angles that measure  and
and  ?
?
Which of the following is true about a triangle with two angles that measure 

The sum of the two given angles is 90 degrees, which means that the third angle should be a right angle (90 degrees). We also know that two of the angles are equal. Therefore, the triangle is right and isosceles.
The sum of the two given angles is 90 degrees, which means that the third angle should be a right angle (90 degrees). We also know that two of the angles are equal. Therefore, the triangle is right and isosceles.
Compare your answer with the correct one above
What is the value of x in a right triangle if the two acute angles are equal to 5x and 25x?
What is the value of x in a right triangle if the two acute angles are equal to 5x and 25x?
In a right triangle, there is one right angle of 90 degrees, while the two acute angles add up to 90 degrees.
Given that the two acute angles are equal to 5x and 25x, the value of x can be calculated with the equation below:



In a right triangle, there is one right angle of 90 degrees, while the two acute angles add up to 90 degrees.
Given that the two acute angles are equal to 5x and 25x, the value of x can be calculated with the equation below:
Compare your answer with the correct one above

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 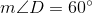 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 



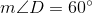

Compare your answer with the correct one above
One angle of a right triangle measures 45 degrees, and the hypotenuse measures 8 centimeters. Give the area of the triangle.
One angle of a right triangle measures 45 degrees, and the hypotenuse measures 8 centimeters. Give the area of the triangle.
This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let  hypotenuse and
hypotenuse and  side length.
side length.


We can then plug this side length into the formula for area.

This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 

We can then plug this side length into the formula for area.
Compare your answer with the correct one above
The legs of a right triangle measure  and
and  . What is its perimeter?
. What is its perimeter?
The legs of a right triangle measure 

The hypotenuse of the triangle can be calculated using the Pythagorean Theorem. Set  :
:





Add the three sidelengths:

The hypotenuse of the triangle can be calculated using the Pythagorean Theorem. Set 
Add the three sidelengths:
Compare your answer with the correct one above

Figure NOT drawn to scale
 is a right triangle with altitude
is a right triangle with altitude  . Give the ratio of the area of
. Give the ratio of the area of  to that of
to that of  .
.

Figure NOT drawn to scale




The altitude of a right triangle from the vertex of its right angle - which, here, is  - divides the triangle into two triangles similar to each other. The ratio of the hypotenuse of the white triangle to that of the gray triangle (which are corresponding sides) is
- divides the triangle into two triangles similar to each other. The ratio of the hypotenuse of the white triangle to that of the gray triangle (which are corresponding sides) is
 ,
,
making this the similarity ratio. The ratio of the areas of two similar triangles is the square of their similarity ratio, which here is
 , or
, or  .
.
The altitude of a right triangle from the vertex of its right angle - which, here, is 

making this the similarity ratio. The ratio of the areas of two similar triangles is the square of their similarity ratio, which here is


Compare your answer with the correct one above
Find the area of a right triangle with a base of 7cm and a height of 20cm.
Find the area of a right triangle with a base of 7cm and a height of 20cm.
To find the area of a right triangle, we will use the following formula:

where b is the base and h is the height of the triangle.
We know the base of the triangle is 7cm. We know the height of the triangle is 20cm. Knowing this, we can substitute into the formula. We get



To find the area of a right triangle, we will use the following formula:
where b is the base and h is the height of the triangle.
We know the base of the triangle is 7cm. We know the height of the triangle is 20cm. Knowing this, we can substitute into the formula. We get
Compare your answer with the correct one above

Refer to the above figure. Evaluate the length of  in terms of
in terms of  .
.

Refer to the above figure. Evaluate the length of 

The altitude of a right triangle to its hypotenuse divides the triangle into two smaller trangles similar to each other and to the large triangle.
Therefore,

and, consequently,
 ,
,
or, equivalently,

 by the Pythagorean Theorem, so
by the Pythagorean Theorem, so
 .
.
The altitude of a right triangle to its hypotenuse divides the triangle into two smaller trangles similar to each other and to the large triangle.
Therefore,
and, consequently,

or, equivalently,


Compare your answer with the correct one above

Refer to the above figure. Evaluate the length of  in terms of
in terms of  .
.

Refer to the above figure. Evaluate the length of 

The height of a right triangle from the vertex of its right angle is the geometric mean - in this case, the square root of the product - of the lengths of the two segments of the hypotenuse that it forms. Therefore,

The height of a right triangle from the vertex of its right angle is the geometric mean - in this case, the square root of the product - of the lengths of the two segments of the hypotenuse that it forms. Therefore,
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
In the above right triangle,  . Give the length of
. Give the length of  .
.

Note: Figure NOT drawn to scale.
In the above right triangle, 

The two triangles formed by an altitude from the vertex of a right triangle are similar to each other and the large triangle, so all three are 30-60-90 triangles. Take advantage of this, applying it twice.
Looking at  . By the 30-60-90 Theorem, the shorter leg of a hypotentuse measures half that of the hypotenuse.
. By the 30-60-90 Theorem, the shorter leg of a hypotentuse measures half that of the hypotenuse.  .
.
Now, look at  . By the same theorem,
. By the same theorem,

and

The two triangles formed by an altitude from the vertex of a right triangle are similar to each other and the large triangle, so all three are 30-60-90 triangles. Take advantage of this, applying it twice.
Looking at 

Now, look at 
and
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
In the above figure,  .
.
Which of the following comes closest to the length of  ?
?

Note: Figure NOT drawn to scale.
In the above figure, 
Which of the following comes closest to the length of 
 and
and  , so by the Pythagorean Theorem,
, so by the Pythagorean Theorem,





Because  is the altitude from the vertex
is the altitude from the vertex  of
of  ,
,
 .
.
Therefore,



Also,



For similar reasons,
 .
.
Therefore,



Of the choices given, 60 comes closest.


Because 



Therefore,
Also,
For similar reasons,

Therefore,
Of the choices given, 60 comes closest.
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above map. A farmer owns a triangular plot of land flanked by the three highways as shown. The farmer uses Highway 2 frequently; however, he can only access it by driving five miles north on Highway 32 or twelve miles east on Highway 100.
He wants to build a dirt road that directly accesses Highway 2. He figures that it will cost $1,500 per tenth of a mile to construct the road. By his estimate, which answer will come closest to the total cost of the shortest possible road?

Note: Figure NOT drawn to scale.
Refer to the above map. A farmer owns a triangular plot of land flanked by the three highways as shown. The farmer uses Highway 2 frequently; however, he can only access it by driving five miles north on Highway 32 or twelve miles east on Highway 100.
He wants to build a dirt road that directly accesses Highway 2. He figures that it will cost $1,500 per tenth of a mile to construct the road. By his estimate, which answer will come closest to the total cost of the shortest possible road?
The three roads form the legs and the hypotenuse of a right triangle with legs 5 and 12 miles; by the Pythagorean Theorem, the hypotenuse is
 miles.
miles.
To find the length of the shortest possible road, which must be perpendicular to Highway 2, it should be observed that this road serves as an altitude from the vertex of the triangle to the hypotenuse.
The area of a right triangle can be calculated two ways - by taking half the product of the lengths of the legs or by taking half the product of the length of the altitude (height) and that of the hypotenuse. Setting  as the height, we can solve for
as the height, we can solve for  in the equation:
in the equation:


 miles.
miles.
This is 46 tenths of a mile, so the approximate cost of the road in dollars will be

Among the five choices, $70,000 comes closest.
The three roads form the legs and the hypotenuse of a right triangle with legs 5 and 12 miles; by the Pythagorean Theorem, the hypotenuse is

To find the length of the shortest possible road, which must be perpendicular to Highway 2, it should be observed that this road serves as an altitude from the vertex of the triangle to the hypotenuse.
The area of a right triangle can be calculated two ways - by taking half the product of the lengths of the legs or by taking half the product of the length of the altitude (height) and that of the hypotenuse. Setting 


This is 46 tenths of a mile, so the approximate cost of the road in dollars will be
Among the five choices, $70,000 comes closest.
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
In the above figure,  .
.
Which of the following comes closest to the length of  ?
?

Note: Figure NOT drawn to scale.
In the above figure, 
Which of the following comes closest to the length of 
 and
and  , so by the Pythagorean Theorem,
, so by the Pythagorean Theorem,





Because  is the altitude from the vertex
is the altitude from the vertex  of
of  ,
,
 .
.
Therefore,



Also,



For similar reasons,
 .
.
Therefore,


 .
.
Of the choices given, 75 comes closest.


Because 



Therefore,
Also,
For similar reasons,

Therefore,

Of the choices given, 75 comes closest.
Compare your answer with the correct one above

Refer to the above diagram, which depicts a right triangle. What is the value of  ?
?

Refer to the above diagram, which depicts a right triangle. What is the value of 
By the Pythagorean Theorem, which says  .
.  being the hypotenuse, or
being the hypotenuse, or  in this problem.
in this problem.




Simply


By the Pythagorean Theorem, which says 


Simply
Compare your answer with the correct one above
If a right triangle has a base of  and a height of
and a height of  , what is the length of the hypotenuse?
, what is the length of the hypotenuse?
If a right triangle has a base of 

To solve this problem, we must utilize the Pythagorean Theorom, which states that:

We know that the base is  , so we can substitute
, so we can substitute  in for
in for  . We also know that the height is
. We also know that the height is  , so we can substitute
, so we can substitute  in for
in for  .
.

Next we evaluate the exponents:


Now we add them together:

Then,  .
.
 is not a perfect square, so we simply write the square root as
is not a perfect square, so we simply write the square root as  .
.

To solve this problem, we must utilize the Pythagorean Theorom, which states that:
We know that the base is 





Next we evaluate the exponents:
Now we add them together:
Then, 


Compare your answer with the correct one above
If a right triangle has a base of  and a height of
and a height of  , what is the length of the hypotenuse?
, what is the length of the hypotenuse?
If a right triangle has a base of 

To solve this problem, we are going to use the Pythagorean Theorom, which states that  .
.
We know that this particular right triangle has a base of  , which can be substituted for
, which can be substituted for  , and a height of
, and a height of  , which can be substituted for
, which can be substituted for  . If we rewrite the theorom using these numbers, we get:
. If we rewrite the theorom using these numbers, we get:

Next, we evaluate the expoenents:




Then,  .
.
To solve for  , we must find the square root of
, we must find the square root of  . Since this is not a perfect square, our answer is simply
. Since this is not a perfect square, our answer is simply  .
.
To solve this problem, we are going to use the Pythagorean Theorom, which states that 
We know that this particular right triangle has a base of 



Next, we evaluate the expoenents:
Then, 
To solve for 


Compare your answer with the correct one above
What is the hypotenuse of a right triangle with sides 5 and 8?
What is the hypotenuse of a right triangle with sides 5 and 8?
According to the Pythagorean Theorem, the equation for the hypotenuse of a right triangle is  . Plugging in the sides, we get
. Plugging in the sides, we get  . Solving for
. Solving for  , we find that the hypotenuse is
, we find that the hypotenuse is  :
:


According to the Pythagorean Theorem, the equation for the hypotenuse of a right triangle is 



Compare your answer with the correct one above
In a right triangle, two sides have length  . Give the length of the hypotenuse in terms of
. Give the length of the hypotenuse in terms of  .
.
In a right triangle, two sides have length 

By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let  hypotenuse and
hypotenuse and  side length.
side length.

By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 

Compare your answer with the correct one above
In a right triangle, two sides have lengths 5 centimeters and 12 centimeters. Give the length of the hypotenuse.
In a right triangle, two sides have lengths 5 centimeters and 12 centimeters. Give the length of the hypotenuse.
This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let  hypotenuse and
hypotenuse and  ,
,  lengths of the other two sides.
lengths of the other two sides.


This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 


Compare your answer with the correct one above
In a rectangle, the width is 6 feet long and the length is 8 feet long. If a diagonal is drawn through the rectangle, from one corner to the other, how many feet long is that diagonal?
In a rectangle, the width is 6 feet long and the length is 8 feet long. If a diagonal is drawn through the rectangle, from one corner to the other, how many feet long is that diagonal?
Given that a rectangle has all right angles, drawing a diagonal will create a right triangle the legs are each 6 feet and 8 feet.
We know that in a 3-4-5 right triangle, when the legs are 3 feet and 4 feet, the hypotenuse will be 5 feet.
Given that the legs of this triangle are twice as long as those in the 3-4-5 triangle, it follows that the hypotense will also be twice as long.
Thus, the diagonal in through the rectangle creates a 6-8-10 triangle. 10 is therefore the length of the diagonal.
Given that a rectangle has all right angles, drawing a diagonal will create a right triangle the legs are each 6 feet and 8 feet.
We know that in a 3-4-5 right triangle, when the legs are 3 feet and 4 feet, the hypotenuse will be 5 feet.
Given that the legs of this triangle are twice as long as those in the 3-4-5 triangle, it follows that the hypotense will also be twice as long.
Thus, the diagonal in through the rectangle creates a 6-8-10 triangle. 10 is therefore the length of the diagonal.
Compare your answer with the correct one above