Trapezoids - ISEE Upper Level Quantitative Reasoning
Card 0 of 36

Find the area of the above trapezoid if  ,
,  , and
, and  .
.
Figure not drawn to scale.

Find the area of the above trapezoid if 


Figure not drawn to scale.
The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.




The area of a trapezoid is given by

where 


Compare your answer with the correct one above
A trapezoid has the base lengths of  and
and  . The area of the trapezoid is
. The area of the trapezoid is  . Give the height of the trapezoid in terms of
. Give the height of the trapezoid in terms of  .
.
A trapezoid has the base lengths of 



The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.


The area of a trapezoid is given by

where 


Compare your answer with the correct one above
In the following trapezoid  and
and  . The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.
. The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.

In the following trapezoid 


The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.



Substitute these values into the area formula:

The area of a trapezoid is given by

where 


Substitute these values into the area formula:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above trapezoid has area  . What is
. What is  ?
?

Note: Figure NOT drawn to scale.
The above trapezoid has area 

Substitute  in the formula for the area of a trapezoid:
in the formula for the area of a trapezoid:






Substitute 
Compare your answer with the correct one above
A trapezoid has height 20 inches. Its bases have sum 30 inches, and one base is 6 inches longer than the other. What is the area of this trapezoid?
A trapezoid has height 20 inches. Its bases have sum 30 inches, and one base is 6 inches longer than the other. What is the area of this trapezoid?
You do not need to find the individual bases; their sum,  , is
, is  . You can substitute
. You can substitute  into the formula for the area of a trapezoid:
into the formula for the area of a trapezoid:

 square inches.
square inches.
Note that the fact that one base is  inches longer is not important here.
inches longer is not important here.
You do not need to find the individual bases; their sum, 



Note that the fact that one base is 
Compare your answer with the correct one above

What is the area of the shaded portion of the above square?

What is the area of the shaded portion of the above square?
Quadrilateral  - the shaded region - is a trapezoid with bases
- the shaded region - is a trapezoid with bases  and
and  , and altitude
, and altitude  . The area of the trapezoid can be calculated using the formula
. The area of the trapezoid can be calculated using the formula
 ,
,
where  and
and  , and
, and  .
.
The length of  can be found by setting
can be found by setting  and
and  and applying the Pythagorean Theorem:
and applying the Pythagorean Theorem:

Therefore,
 .
.
Substituting:




Quadrilateral 




where 


The length of 


Therefore,

Substituting:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 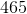 . What is
. What is  ?
?

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 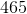

Substitute  into the formula for the area of a trapezoid:
into the formula for the area of a trapezoid:




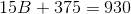

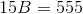
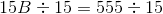

Substitute 
Compare your answer with the correct one above
The perimeter of the following trapezoid is  .
.
The following is given:




Find  .
.
Figure not drawn to scale.

The perimeter of the following trapezoid is 
The following is given:
Find 
Figure not drawn to scale.

The perimeter of a trapezoid is equal to the sum of all of the sides, i.e.
 ,
,
where  are the lengths of each side.
are the lengths of each side.

The perimeter of a trapezoid is equal to the sum of all of the sides, i.e.

where 
Compare your answer with the correct one above
The bigger base length of a trapezoid is two times bigger than the smaller base length. Legs of the trapezoid have the same length of  . If the perimeter of the trapezoid is
. If the perimeter of the trapezoid is  , give the length of the smaller base.
, give the length of the smaller base.
The bigger base length of a trapezoid is two times bigger than the smaller base length. Legs of the trapezoid have the same length of 

Like any polygon, the perimeter of a trapezoid is the total distance around the outside, i.e.
 ,
,
where  are the lengths of each side.
are the lengths of each side.
Let  small base length and
small base length and  big base length.
big base length.

Like any polygon, the perimeter of a trapezoid is the total distance around the outside, i.e.

where 
Let 

Compare your answer with the correct one above

Find the area of the above trapezoid if  ,
,  , and
, and  .
.
Figure not drawn to scale.

Find the area of the above trapezoid if 


Figure not drawn to scale.
The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.




The area of a trapezoid is given by

where 


Compare your answer with the correct one above
A trapezoid has the base lengths of  and
and  . The area of the trapezoid is
. The area of the trapezoid is  . Give the height of the trapezoid in terms of
. Give the height of the trapezoid in terms of  .
.
A trapezoid has the base lengths of 



The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.


The area of a trapezoid is given by

where 


Compare your answer with the correct one above
In the following trapezoid  and
and  . The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.
. The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.

In the following trapezoid 


The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.



Substitute these values into the area formula:

The area of a trapezoid is given by

where 


Substitute these values into the area formula:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above trapezoid has area  . What is
. What is  ?
?

Note: Figure NOT drawn to scale.
The above trapezoid has area 

Substitute  in the formula for the area of a trapezoid:
in the formula for the area of a trapezoid:






Substitute 
Compare your answer with the correct one above
A trapezoid has height 20 inches. Its bases have sum 30 inches, and one base is 6 inches longer than the other. What is the area of this trapezoid?
A trapezoid has height 20 inches. Its bases have sum 30 inches, and one base is 6 inches longer than the other. What is the area of this trapezoid?
You do not need to find the individual bases; their sum,  , is
, is  . You can substitute
. You can substitute  into the formula for the area of a trapezoid:
into the formula for the area of a trapezoid:

 square inches.
square inches.
Note that the fact that one base is  inches longer is not important here.
inches longer is not important here.
You do not need to find the individual bases; their sum, 



Note that the fact that one base is 
Compare your answer with the correct one above

What is the area of the shaded portion of the above square?

What is the area of the shaded portion of the above square?
Quadrilateral  - the shaded region - is a trapezoid with bases
- the shaded region - is a trapezoid with bases  and
and  , and altitude
, and altitude  . The area of the trapezoid can be calculated using the formula
. The area of the trapezoid can be calculated using the formula
 ,
,
where  and
and  , and
, and  .
.
The length of  can be found by setting
can be found by setting  and
and  and applying the Pythagorean Theorem:
and applying the Pythagorean Theorem:

Therefore,
 .
.
Substituting:




Quadrilateral 




where 


The length of 


Therefore,

Substituting:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 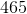 . What is
. What is  ?
?

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 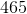

Substitute  into the formula for the area of a trapezoid:
into the formula for the area of a trapezoid:




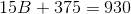

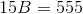
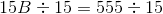

Substitute 
Compare your answer with the correct one above
The perimeter of the following trapezoid is  .
.
The following is given:




Find  .
.
Figure not drawn to scale.

The perimeter of the following trapezoid is 
The following is given:
Find 
Figure not drawn to scale.

The perimeter of a trapezoid is equal to the sum of all of the sides, i.e.
 ,
,
where  are the lengths of each side.
are the lengths of each side.

The perimeter of a trapezoid is equal to the sum of all of the sides, i.e.

where 
Compare your answer with the correct one above
The bigger base length of a trapezoid is two times bigger than the smaller base length. Legs of the trapezoid have the same length of  . If the perimeter of the trapezoid is
. If the perimeter of the trapezoid is  , give the length of the smaller base.
, give the length of the smaller base.
The bigger base length of a trapezoid is two times bigger than the smaller base length. Legs of the trapezoid have the same length of 

Like any polygon, the perimeter of a trapezoid is the total distance around the outside, i.e.
 ,
,
where  are the lengths of each side.
are the lengths of each side.
Let  small base length and
small base length and  big base length.
big base length.

Like any polygon, the perimeter of a trapezoid is the total distance around the outside, i.e.

where 
Let 

Compare your answer with the correct one above

Find the area of the above trapezoid if  ,
,  , and
, and  .
.
Figure not drawn to scale.

Find the area of the above trapezoid if 


Figure not drawn to scale.
The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.




The area of a trapezoid is given by

where 


Compare your answer with the correct one above
A trapezoid has the base lengths of  and
and  . The area of the trapezoid is
. The area of the trapezoid is  . Give the height of the trapezoid in terms of
. Give the height of the trapezoid in terms of  .
.
A trapezoid has the base lengths of 



The area of a trapezoid is given by
 ,
,
where  ,
,  are the lengths of each base and
are the lengths of each base and  is the altitude (height) of the trapezoid.
is the altitude (height) of the trapezoid.


The area of a trapezoid is given by

where 


Compare your answer with the correct one above