How to find the length of the diagonal of a kite - ISEE Upper Level Quantitative Reasoning
Card 0 of 4
A kite has the area of  . One of the diagonals of the kite has length
. One of the diagonals of the kite has length  . Give the length of the other diagonal of the kite.
. Give the length of the other diagonal of the kite.
A kite has the area of 

The area of a kite is half the product of the diagonals, i.e.
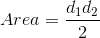 ,
,
where  and
and  are the lengths of the diagonals.
are the lengths of the diagonals.

The area of a kite is half the product of the diagonals, i.e.
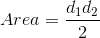
where 

Compare your answer with the correct one above
A kite has the area of  . One of the diagonals of the kite has length
. One of the diagonals of the kite has length  . Give the length of the other diagonal of the kite.
. Give the length of the other diagonal of the kite.
A kite has the area of 

The area of a kite is half the product of the diagonals, i.e.
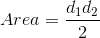 ,
,
where  and
and  are the lengths of the diagonals.
are the lengths of the diagonals.

The area of a kite is half the product of the diagonals, i.e.
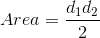
where 

Compare your answer with the correct one above
A kite has the area of  . One of the diagonals of the kite has length
. One of the diagonals of the kite has length  . Give the length of the other diagonal of the kite.
. Give the length of the other diagonal of the kite.
A kite has the area of 

The area of a kite is half the product of the diagonals, i.e.
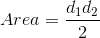 ,
,
where  and
and  are the lengths of the diagonals.
are the lengths of the diagonals.

The area of a kite is half the product of the diagonals, i.e.
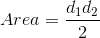
where 

Compare your answer with the correct one above
A kite has the area of  . One of the diagonals of the kite has length
. One of the diagonals of the kite has length  . Give the length of the other diagonal of the kite.
. Give the length of the other diagonal of the kite.
A kite has the area of 

The area of a kite is half the product of the diagonals, i.e.
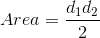 ,
,
where  and
and  are the lengths of the diagonals.
are the lengths of the diagonals.

The area of a kite is half the product of the diagonals, i.e.
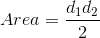
where 

Compare your answer with the correct one above