How to find the area of a hexagon - ISEE Upper Level Quantitative Reasoning
Card 0 of 4
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
A regular hexagon with sidelength 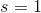 can be seen as a composite of six equilateral triangles, each with sidelength
can be seen as a composite of six equilateral triangles, each with sidelength  . Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength
. Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength  is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
A regular hexagon with sidelength 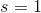


Compare your answer with the correct one above
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
A regular hexagon with sidelength 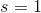 can be seen as a composite of six equilateral triangles, each with sidelength
can be seen as a composite of six equilateral triangles, each with sidelength  . Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength
. Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength  is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
A regular hexagon with sidelength 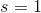


Compare your answer with the correct one above
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
A regular hexagon with sidelength 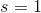 can be seen as a composite of six equilateral triangles, each with sidelength
can be seen as a composite of six equilateral triangles, each with sidelength  . Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength
. Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength  is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
A regular hexagon with sidelength 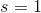


Compare your answer with the correct one above
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
A regular hexagon with sidelength 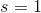 can be seen as a composite of six equilateral triangles, each with sidelength
can be seen as a composite of six equilateral triangles, each with sidelength  . Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength
. Since area is in direct proportion to the square of the sidelength, the area of the equilateral triangle with sidelength  is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
is equal to that of four of those triangles. This makes the hexagon greater in area, and it makes (a) the greater quantity.
A regular hexagon with sidelength 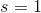


Compare your answer with the correct one above