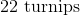How to find the solution to an equation
Help Questions
ISEE Lower Level Quantitative Reasoning › How to find the solution to an equation
Five more than a number is equal to 
Explanation
From the question, we know that 








The number we are looking for needs to be five less than 

You can also solve this algebraically by setting up this equation and solving:
Subtract 
4 puppies from a litter are adopted, and 
Explanation
If 

Set up a proportion and solve:
Therefore, there are 6 puppies total in the litter.
What is the value of 
Explanation
In order to solve for 

This results in:
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
What is the value of h in the expression below?
Explanation
The steps for solving the equation, 
First, multiply 3 by the components of the parentheses.
Subtract 12 from each side.
Divide each side by 15.
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Solve for 
Explanation
To solve an equation, first combine like terms. Move the 

Next, remove the 

The answer is 
Which of the following phrases can be written as the algebraic expression 
The quotient of a number and seven subtracted from ten
Ten subtracted from the quotient of a number and seven
The quotient of seven and a number subtracted from ten
The difference of a number and ten divided by seven
The difference of a number and ten divided into seven
Explanation




Therefore,