Infinite Series of Functions - Introduction to Analysis
Card 0 of 4
Determine whether the following statement is true or false:
Some power series such as  have a possible radius of convergence that can be found by computing the roots of the coefficients of
have a possible radius of convergence that can be found by computing the roots of the coefficients of  .
.
Determine whether the following statement is true or false:
Some power series such as 

This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When  is fixed,
is fixed,  , and
, and 
with the assumption that  and
and  the Root Test is applied to the series
the Root Test is applied to the series  .
.
When 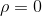 by the assumption and the notation that
by the assumption and the notation that

implies that  therefore by the Root Test,
therefore by the Root Test,  does not converge for any
does not converge for any  and thus the radius of convergence of
and thus the radius of convergence of  is
is  .
.
This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When 

with the assumption that 


When 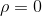
implies that 




Compare your answer with the correct one above
Determine whether the following statement is true or false:
Some power series such as  have a possible radius of convergence that can be found by computing the roots of the coefficients of
have a possible radius of convergence that can be found by computing the roots of the coefficients of  .
.
Determine whether the following statement is true or false:
Some power series such as 

This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When  is fixed,
is fixed,  , and
, and 
with the assumption that  and
and  the Root Test is applied to the series
the Root Test is applied to the series  .
.
When 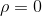 by the assumption and the notation that
by the assumption and the notation that

implies that  therefore by the Root Test,
therefore by the Root Test,  does not converge for any
does not converge for any  and thus the radius of convergence of
and thus the radius of convergence of  is
is  .
.
This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When 

with the assumption that 


When 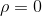
implies that 




Compare your answer with the correct one above
Determine whether the following statement is true or false:
Some power series such as  have a possible radius of convergence that can be found by computing the roots of the coefficients of
have a possible radius of convergence that can be found by computing the roots of the coefficients of  .
.
Determine whether the following statement is true or false:
Some power series such as 

This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When  is fixed,
is fixed,  , and
, and 
with the assumption that  and
and  the Root Test is applied to the series
the Root Test is applied to the series  .
.
When 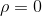 by the assumption and the notation that
by the assumption and the notation that

implies that  therefore by the Root Test,
therefore by the Root Test,  does not converge for any
does not converge for any  and thus the radius of convergence of
and thus the radius of convergence of  is
is  .
.
This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When 

with the assumption that 


When 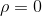
implies that 




Compare your answer with the correct one above
Determine whether the following statement is true or false:
Some power series such as  have a possible radius of convergence that can be found by computing the roots of the coefficients of
have a possible radius of convergence that can be found by computing the roots of the coefficients of  .
.
Determine whether the following statement is true or false:
Some power series such as 

This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When  is fixed,
is fixed,  , and
, and 
with the assumption that  and
and  the Root Test is applied to the series
the Root Test is applied to the series  .
.
When 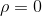 by the assumption and the notation that
by the assumption and the notation that

implies that  therefore by the Root Test,
therefore by the Root Test,  does not converge for any
does not converge for any  and thus the radius of convergence of
and thus the radius of convergence of  is
is  .
.
This statement is false because every power series has a radius of convergence that is found by computing the roots the series coefficients.
The proof of one case is as follows:
When 

with the assumption that 


When 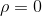
implies that 




Compare your answer with the correct one above