Measurement and Geometry - HiSET
Card 0 of 536
Given:  and
and  such that
such that  .
.
Does sufficient information exist to prove that  , and if so, by what postulate or theorem?
, and if so, by what postulate or theorem?
Given: 


Does sufficient information exist to prove that 
We are given that, between the triangles, two pairs of corresponding sides are proportional. Without knowing anything else, the proportionality of two pairs of sides is insufficient to prove that the triangles are similar.
We are given that, between the triangles, two pairs of corresponding sides are proportional. Without knowing anything else, the proportionality of two pairs of sides is insufficient to prove that the triangles are similar.
Compare your answer with the correct one above
Given:  and
and  such that
such that  and
and  .
.
Does sufficient information exist to prove that  , and if so, by what postulate or theorem?
, and if so, by what postulate or theorem?
Given: 



Does sufficient information exist to prove that 
We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. The angles that are congruent are the included angles of their respective sides. By the SAS Similarity Postulate, this is enough to prove that  .
.
We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. The angles that are congruent are the included angles of their respective sides. By the SAS Similarity Postulate, this is enough to prove that 
Compare your answer with the correct one above
Given:  and
and  such that
such that  and
and  .
.
Does sufficient information exist to prove that  , and if so, by what postulate or theorem?
, and if so, by what postulate or theorem?
Given: 



Does sufficient information exist to prove that 
We are given that, between the triangles, two pairs of corresponding angles are congruent. By the AA Similarity Postulate, this is enough to prove that  .
.
We are given that, between the triangles, two pairs of corresponding angles are congruent. By the AA Similarity Postulate, this is enough to prove that 
Compare your answer with the correct one above
Given:  and
and  such that
such that  and
and  .
.
Does sufficient information exist to prove that  , and if so, by what postulate or theorem?
, and if so, by what postulate or theorem?
Given: 



Does sufficient information exist to prove that 
We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. If the angles were the included angles of the triangles, then the SAS Similarity Theorem could be applied to prove that  ; however, the two congruent angles are nonincluded, and there is no "SSA" statement that can be applied to prove similarity. Without further information, it cannot be proved that the triangles are similar.
; however, the two congruent angles are nonincluded, and there is no "SSA" statement that can be applied to prove similarity. Without further information, it cannot be proved that the triangles are similar.
We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. If the angles were the included angles of the triangles, then the SAS Similarity Theorem could be applied to prove that 
Compare your answer with the correct one above
 with scale factor 4:5, with
with scale factor 4:5, with  the smaller triangle.
the smaller triangle.
Complete the sentence: the perimeter of  is % less than that of
is % less than that of  .
.
(Select the closest whole percent)


Complete the sentence: the perimeter of 

(Select the closest whole percent)
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is  .
.
This makes the perimeter of the smaller triangle  equal to
equal to  of that of larger triangle
of that of larger triangle  —or, equivalently,
—or, equivalently,  less.
less.
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is 
This makes the perimeter of the smaller triangle 



Compare your answer with the correct one above
 with scale factor 5:4, with
with scale factor 5:4, with  the larger triangle.
the larger triangle.
Complete the sentence: the perimeter of  is % greater than that of
is % greater than that of  .
.
(Select the closest whole percent).


Complete the sentence: the perimeter of 

(Select the closest whole percent).
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is  .
.
This makes the perimeter of larger triangle  equal to
equal to  of that of smaller triangle
of that of smaller triangle  —or, equivalently, 25% greater.
—or, equivalently, 25% greater.
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is 
This makes the perimeter of larger triangle 


Compare your answer with the correct one above
 with scale factor 4:5, with
with scale factor 4:5, with  the smaller triangle.
the smaller triangle.
Complete the sentence: the area of  is % less than that of
is % less than that of  .
.
(Select the closest whole percent).


Complete the sentence: the area of 

(Select the closest whole percent).
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to  , so the ratio of the areas is the square of this, or
, so the ratio of the areas is the square of this, or  .
.
This makes the area of smaller triangle  equal to
equal to  of that of larger triangle
of that of larger triangle  —or, equivalently,
—or, equivalently,  less.
less.
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to 

This makes the area of smaller triangle 



Compare your answer with the correct one above
 with scale factor 5:4, with
with scale factor 5:4, with  the larger triangle.
the larger triangle.
Complete the sentence: the area of  is % greater than that of
is % greater than that of  .
.
(Select the closest whole percent)


Complete the sentence: the area of 

(Select the closest whole percent)
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to  , so the ratio of the areas is the square of this, or
, so the ratio of the areas is the square of this, or  .
.
This makes the area of larger triangle  equal to
equal to  of that of smaller triangle
of that of smaller triangle  —or, equivalently,
—or, equivalently,  greater.
greater.
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to 

This makes the area of larger triangle 



Compare your answer with the correct one above
A triangle has sides of length 8 and 12; the triangle is scalene and obtuse. Which of the following could be the length of its third side?
A triangle has sides of length 8 and 12; the triangle is scalene and obtuse. Which of the following could be the length of its third side?
A scalene triangle has three sides of different lengths. The triangle is known to have sides of length 8 and 12, so this eliminates 8 and 12 as the correct choices for the length of the third side.
The sum of the lengths of the two smallest sides must exceed the length of the third side. 4 can be eliminated as a the correct choice, since  , violating this condition.
, violating this condition.
This leaves 6 and 10 as possible answers. For a triangle to be obtuse, it must hold that if  are its sidelengths,
are its sidelengths,  the greatest of the three,
the greatest of the three,
 .
.
If the length of the third side is 10, setting  , we see that
, we see that
 ,
,
violating this condition.
If the length of the third side is 6, setting  , we see that
, we see that
 ,
,
satisfying this condition.
This makes 6 the correct choice.
A scalene triangle has three sides of different lengths. The triangle is known to have sides of length 8 and 12, so this eliminates 8 and 12 as the correct choices for the length of the third side.
The sum of the lengths of the two smallest sides must exceed the length of the third side. 4 can be eliminated as a the correct choice, since 
This leaves 6 and 10 as possible answers. For a triangle to be obtuse, it must hold that if 


If the length of the third side is 10, setting 

violating this condition.
If the length of the third side is 6, setting 

satisfying this condition.
This makes 6 the correct choice.
Compare your answer with the correct one above
Two of the angles of a triangle are congruent; the third has measure ten degrees greater than either one of the first two. What is the measure of the third angle?
Two of the angles of a triangle are congruent; the third has measure ten degrees greater than either one of the first two. What is the measure of the third angle?
Let  be the measure of the third angle. Since its measure is ten degrees greater than either of the others, then the common measure of the other two is
be the measure of the third angle. Since its measure is ten degrees greater than either of the others, then the common measure of the other two is  . The sum of the measures of the angles of a triangle is 180 degrees, so
. The sum of the measures of the angles of a triangle is 180 degrees, so

To solve for  , first ungroup and collect like terms:
, first ungroup and collect like terms:



Isolate  ; first add 20:
; first add 20:


Divide by 3:

Since  ,
,
 .
.
The third angle measures  .
.
Let 

To solve for 
Isolate 
Divide by 3:
Since 

The third angle measures 
Compare your answer with the correct one above
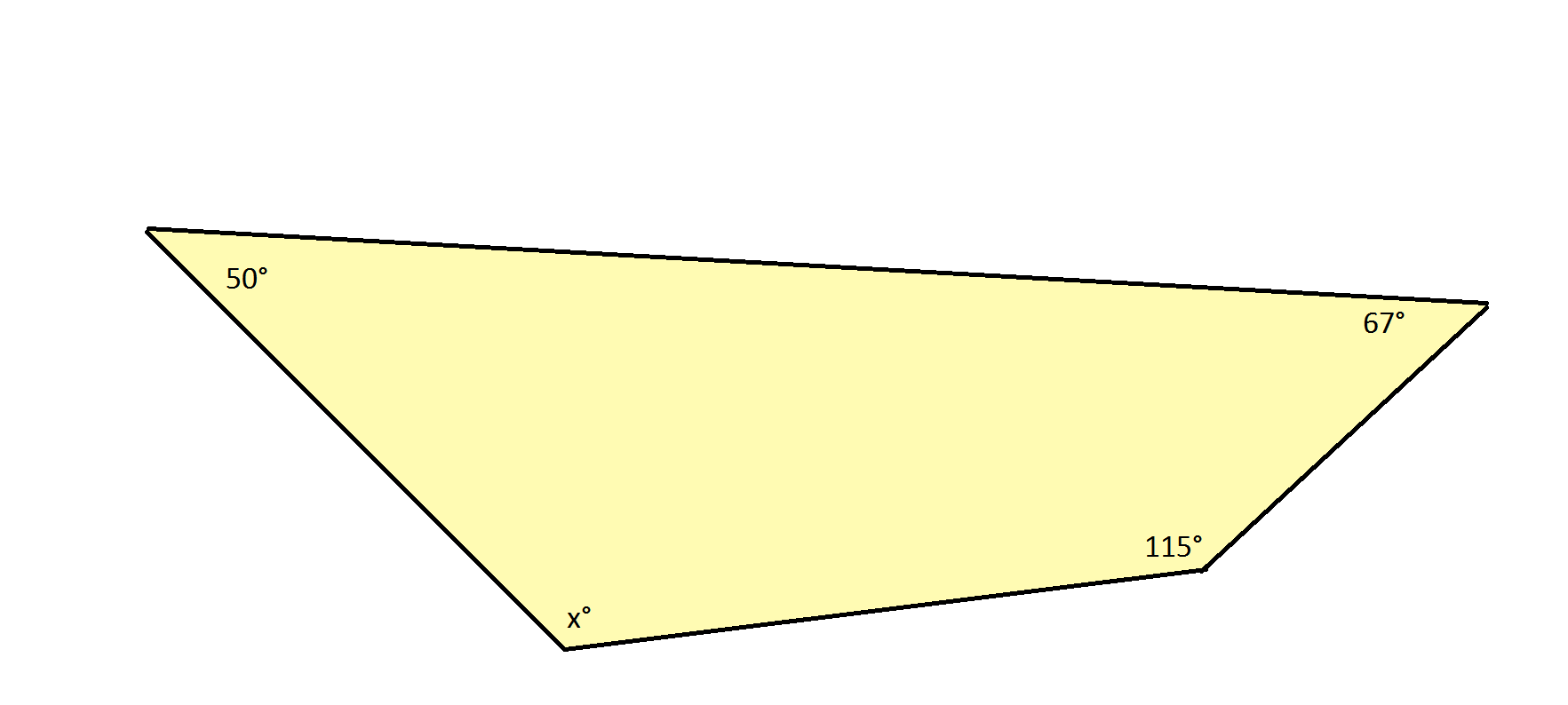
A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.

A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.
The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:
 , where
, where  is the number of sides.
is the number of sides.
For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:

Solving for  requires setting up an algebraic equation, adding all 4 angles to equal 360 degrees:
requires setting up an algebraic equation, adding all 4 angles to equal 360 degrees:

Solving for  is straightforward: subtract the values of the 3 known angles from both sides:
is straightforward: subtract the values of the 3 known angles from both sides:


The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:


For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:
Solving for 
Solving for 
Compare your answer with the correct one above
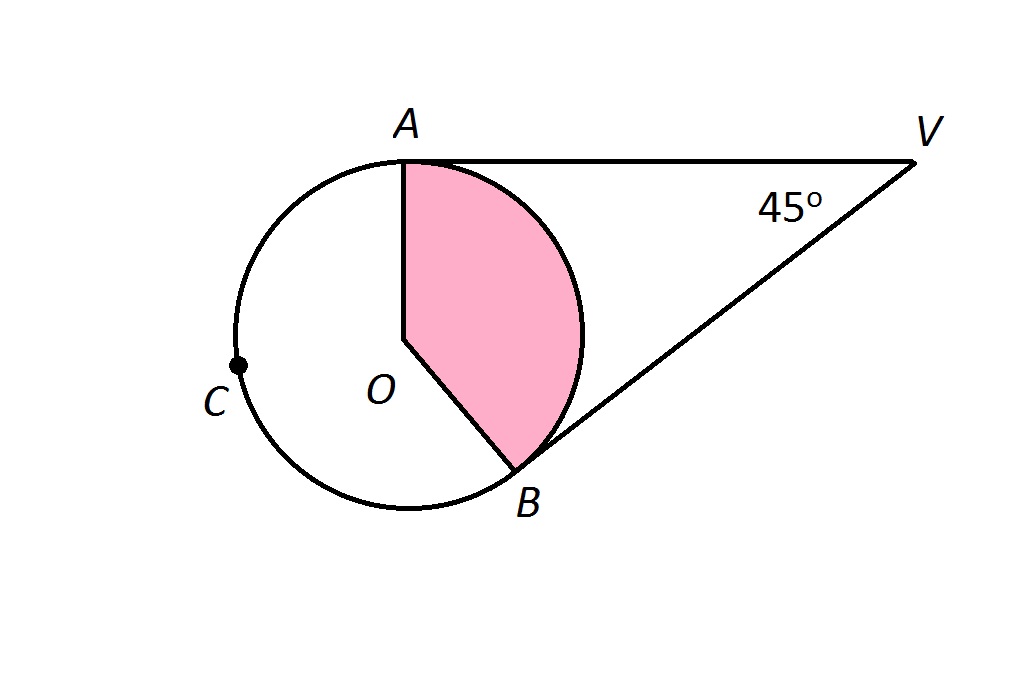
 is the center of the above circle. Calculate
is the center of the above circle. Calculate  .
.



 is the central angle that intercepts
is the central angle that intercepts  , so
, so
 .
.
Therefore, we need to find  to obtain our answer.
to obtain our answer.
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Subtract 360 from both sides:


Divide both sides by  :
:

 ,
,
the measure of  and, consequently, that of
and, consequently, that of  .
.



Therefore, we need to find 
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the measure of 

Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Consider the figure below, which adds some radii of the heptagon (and circle):

 , as a radius of a regular polygon, bisects
, as a radius of a regular polygon, bisects  . The measure of this angle can be calculated using the formula
. The measure of this angle can be calculated using the formula
 ,
,
where  :
:

Consequently,
 ,
,
the correct response.
Consider the figure below, which adds some radii of the heptagon (and circle):




where 
Consequently,

the correct response.
Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into three congruent angles, one of which is
into three congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure three times this; that is,
has measure three times this; that is,

Examine the diagram below, which divides 


The measure of a central angle of a regular 





Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into two congruent angles, one of which is
into two congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure twice this; that is,
has measure twice this; that is,

Examine the diagram below, which divides 


The measure of a central angle of a regular 





Compare your answer with the correct one above

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into two congruent angles, one of which is
into two congruent angles, one of which is  :
:
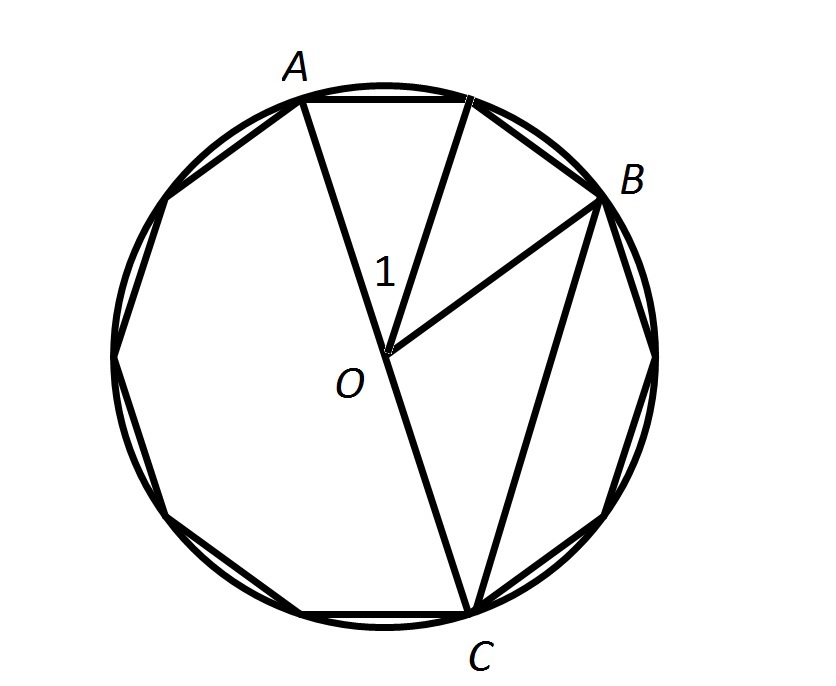
The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure twice this; that is,
has measure twice this; that is,
 .
.
Examine the diagram below, which divides 


The measure of a central angle of a regular 






Compare your answer with the correct one above

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Consider the triangle  . Since
. Since  and
and  are radii, they are congruent, and by the Isosceles Triangle Theorem,
are radii, they are congruent, and by the Isosceles Triangle Theorem,  .
.
Now, examine the figure below, which divides  into three congruent angles, one of which is
into three congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure three times this; that is,
has measure three times this; that is,
 .
.
The measures of the interior angles of a triangle total  , so
, so

Substituting 108 for  and
and  for
for  :
:






Consider the triangle 



Now, examine the figure below, which divides 


The measure of a central angle of a regular 






The measures of the interior angles of a triangle total 
Substituting 108 for 


Compare your answer with the correct one above

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Through symmetry, it can be seen that Quadrilateral  is a trapezoid, such that
is a trapezoid, such that  . By the Same-Side Interior Angle Theorem,
. By the Same-Side Interior Angle Theorem,  and
and  are supplementary - that is,
are supplementary - that is,
 .
.
The measure of  can be calculated using the formula
can be calculated using the formula
 ,
,
where  :
:

Substituting:



Through symmetry, it can be seen that Quadrilateral 




The measure of 

where 
Substituting:
Compare your answer with the correct one above
If two angles are supplementary and one angle measures  , what is the measurement of the second angle?
, what is the measurement of the second angle?
If two angles are supplementary and one angle measures 
Step 1: Define supplementary angles. Supplementary angles are two angles whose sum is  .
.
Step 2: Find the other angle by subtracting the given angle from the maximum sum of the two angles.
So, 
The missing angle (or second angle) is 
Step 1: Define supplementary angles. Supplementary angles are two angles whose sum is 
Step 2: Find the other angle by subtracting the given angle from the maximum sum of the two angles.
So,
The missing angle (or second angle) is
Compare your answer with the correct one above
 and
and  are complementary angles.
are complementary angles.
 and
and  are supplementary angles.
are supplementary angles.


Evaluate  .
.




Evaluate 
 and
and  are supplementary angles, so, by definition,
are supplementary angles, so, by definition,

 , so substitute and solve for
, so substitute and solve for  :
:



 and
and  are complementary angles, so, by definition,
are complementary angles, so, by definition,

Substitute and solve for  :
:



 - that is, the angles have the same measure. Therefore,
- that is, the angles have the same measure. Therefore,
 .
.






Substitute and solve for 


Compare your answer with the correct one above




































