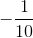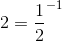The bases don't match.

However:

and we recognize that .

Anything raised to negative power means over the base raised to the postive exponent.

.

Since we can write .

With same base we can set up an equation of

Divide both sides by and we get .

can be written as

Since there is a common base of , we can say

or .

The basees don't match.

However:

thus we can rewrite the expression as .

Anything raised to negative power means over the base raised to the postive exponent.

So, . .

Recall that .

With same base, we can write this equation:

.

By subtracting on both sides, .

First rewrite the two expressions so that they have the same base, and then compare their exponents.

Combine exponents by multiplying:

This is the same as the first given expression, so the two expressions are equal.

We still don't have the same base however:

Then,

.

With same base we can set up an equation of .

Divide both sides by and we get .

Since we can rewrite the expression.

With same base, let's set up an equation of .

By subtracting on both sides, we get .

Take the square root of both sides we get BOTH and .

They don't have the same base, however: .

Then . You would multiply the and the instead of adding.

.

There are two ways to go about this.

Method

They don't have the same bases however: . Then

You would multiply the and the instead of adding. We have

Divide on both sides to get .

Method :

We can change the base from to

This is the basic property of the product of power exponents.

We have the same base so basically .