Evaluating Limits - GRE Quantitative Reasoning
Card 0 of 4
Evaluate: 
Evaluate:
Step 1: See if we can plug in  into the equation..
into the equation..
We can't because the denominator becomes  ..
..
Step 2: Factor the denominator:
 (By the Difference of Perfect Squares Formula)
(By the Difference of Perfect Squares Formula)
Step 3: Re-write the function:
![\frac {(x-2)}{[(x-2)(x+2)]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725550/gif.latex)
Step 4: Divide by  on both the numerator and denominator because it's common:
on both the numerator and denominator because it's common:
We are left with: 
Step 5: Plug in  :
:
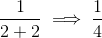
The limit of this function as x approaches 2 is  .
.
Step 1: See if we can plug in 
We can't because the denominator becomes 
Step 2: Factor the denominator:

Step 3: Re-write the function:
Step 4: Divide by 
We are left with:
Step 5: Plug in 
The limit of this function as x approaches 2 is 
Compare your answer with the correct one above
Evaluate: 
Evaluate:
Step 1: See if we can plug in  into the equation..
into the equation..
We can't because the denominator becomes  ..
..
Step 2: Factor the denominator:
 (By the Difference of Perfect Squares Formula)
(By the Difference of Perfect Squares Formula)
Step 3: Re-write the function:
![\frac {(x-2)}{[(x-2)(x+2)]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725550/gif.latex)
Step 4: Divide by  on both the numerator and denominator because it's common:
on both the numerator and denominator because it's common:
We are left with: 
Step 5: Plug in  :
:
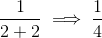
The limit of this function as x approaches 2 is  .
.
Step 1: See if we can plug in 
We can't because the denominator becomes 
Step 2: Factor the denominator:

Step 3: Re-write the function:
Step 4: Divide by 
We are left with:
Step 5: Plug in 
The limit of this function as x approaches 2 is 
Compare your answer with the correct one above
Evaluate: 
Evaluate:
Step 1: See if we can plug in  into the equation..
into the equation..
We can't because the denominator becomes  ..
..
Step 2: Factor the denominator:
 (By the Difference of Perfect Squares Formula)
(By the Difference of Perfect Squares Formula)
Step 3: Re-write the function:
![\frac {(x-2)}{[(x-2)(x+2)]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725550/gif.latex)
Step 4: Divide by  on both the numerator and denominator because it's common:
on both the numerator and denominator because it's common:
We are left with: 
Step 5: Plug in  :
:
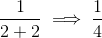
The limit of this function as x approaches 2 is  .
.
Step 1: See if we can plug in 
We can't because the denominator becomes 
Step 2: Factor the denominator:

Step 3: Re-write the function:
Step 4: Divide by 
We are left with:
Step 5: Plug in 
The limit of this function as x approaches 2 is 
Compare your answer with the correct one above
Evaluate: 
Evaluate:
Step 1: See if we can plug in  into the equation..
into the equation..
We can't because the denominator becomes  ..
..
Step 2: Factor the denominator:
 (By the Difference of Perfect Squares Formula)
(By the Difference of Perfect Squares Formula)
Step 3: Re-write the function:
![\frac {(x-2)}{[(x-2)(x+2)]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725550/gif.latex)
Step 4: Divide by  on both the numerator and denominator because it's common:
on both the numerator and denominator because it's common:
We are left with: 
Step 5: Plug in  :
:
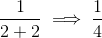
The limit of this function as x approaches 2 is  .
.
Step 1: See if we can plug in 
We can't because the denominator becomes 
Step 2: Factor the denominator:

Step 3: Re-write the function:
Step 4: Divide by 
We are left with:
Step 5: Plug in 
The limit of this function as x approaches 2 is 
Compare your answer with the correct one above