Sectors - GRE Quantitative Reasoning
Card 0 of 120
An ant begins at the center of a pie with a 12" radius. Walking out to the edge of pie, it then proceeds along the outer edge for a certain distance. At a certain point, it turns back toward the center of the pie and returns to the center point. Its whole trek was 55.3 inches. What is the approximate size of the angle through which it traveled?
An ant begins at the center of a pie with a 12" radius. Walking out to the edge of pie, it then proceeds along the outer edge for a certain distance. At a certain point, it turns back toward the center of the pie and returns to the center point. Its whole trek was 55.3 inches. What is the approximate size of the angle through which it traveled?
Tap to see back →
To solve this, we must ascertain the following:
-
The arc length through which the ant traveled.
-
The percentage of the total circumference in light of that arc length.
-
The percentage of 360° proportionate to that arc percentage.
To begin, let's note that the ant travelled 12 + 12 + x inches, where x is the outer arc distance. (It traveled the radius twice, remember); therefore, we know that 24 + x = 55.3 or x = 31.3.
Now, the total circumference of the circle is 2πr or 24π. The arc is 31.3/24π percent of the total circumference; therefore, the percentage of the angle is 360 * 31.3/24π. Since the answers are approximations, use 3.14 for π. This would be 149.52°.
To solve this, we must ascertain the following:
-
The arc length through which the ant traveled.
-
The percentage of the total circumference in light of that arc length.
-
The percentage of 360° proportionate to that arc percentage.
To begin, let's note that the ant travelled 12 + 12 + x inches, where x is the outer arc distance. (It traveled the radius twice, remember); therefore, we know that 24 + x = 55.3 or x = 31.3.
Now, the total circumference of the circle is 2πr or 24π. The arc is 31.3/24π percent of the total circumference; therefore, the percentage of the angle is 360 * 31.3/24π. Since the answers are approximations, use 3.14 for π. This would be 149.52°.
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.

Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.

Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
Tap to see back →
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
A group of students ate an  -inch pizza that was cut into
-inch pizza that was cut into  equal slices. What was the angle measure needed to cut this pizza into these equal slices?
equal slices. What was the angle measure needed to cut this pizza into these equal slices?
A group of students ate an 

Tap to see back →
You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were  slices. If the slices were evenly divided among the
slices. If the slices were evenly divided among the  degrees of the pizza, this means that the degree measure of each slice was
degrees of the pizza, this means that the degree measure of each slice was  . This reduces to
. This reduces to  degrees.
degrees.
You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were 



John owns 8 black shirts, 7 red shirts, 6 blue shirts and 4 white shirts. If he wants to make a circle chart of his shirts, what is the degree angle corresponding to the "blue shirt section?"
John owns 8 black shirts, 7 red shirts, 6 blue shirts and 4 white shirts. If he wants to make a circle chart of his shirts, what is the degree angle corresponding to the "blue shirt section?"
Tap to see back →
We can set up a ratio to calculate the angle measure as such: 6/25 = x/360, since there are 360 degrees in a circle. Solving, we obtain x = 86.4 degrees.
We can set up a ratio to calculate the angle measure as such: 6/25 = x/360, since there are 360 degrees in a circle. Solving, we obtain x = 86.4 degrees.
A circular pie is cut into 30 pieces. Two people wish to split a piece of the pie, but one person wants to have twice as much as the other person. What is the angle of the smaller piece produced in this manner?
A circular pie is cut into 30 pieces. Two people wish to split a piece of the pie, but one person wants to have twice as much as the other person. What is the angle of the smaller piece produced in this manner?
Tap to see back →
First of all, calculate the angle of each of the full pieces of pie. This is easily found:

Though small, this is what the information tells us! Now, we know that if two people are eating the piece, with one having twice the amount of the other, the angles must be  for the smaller piece and
for the smaller piece and  for the larger one. Thus, we can write the equation:
for the larger one. Thus, we can write the equation:

Simplifying, we get:


That is a tiny piece, but that is what is called for by the data!
First of all, calculate the angle of each of the full pieces of pie. This is easily found:
Though small, this is what the information tells us! Now, we know that if two people are eating the piece, with one having twice the amount of the other, the angles must be 

Simplifying, we get:
That is a tiny piece, but that is what is called for by the data!
Quantity A: The angle of a circle's sector having an arc length of  and a radius of
and a radius of  .
.
Quantity B: The angle of a circle's sector having an area of  and a radius of
and a radius of  .
.
Which of the following relations is true?
Quantity A: The angle of a circle's sector having an arc length of 

Quantity B: The angle of a circle's sector having an area of 

Which of the following relations is true?
Tap to see back →
For each of these, you need to compute the total measurement applicable to the given data. For Quantity A, this will be the total circumference. For Quantity B, this will be the total area. You will then divide the given sector calculation by this total amount. By multiplying this percentage by  , you will find the degree measure of each; however, you will merely need to stop at the percentage (since both are percentages of the same number, namely
, you will find the degree measure of each; however, you will merely need to stop at the percentage (since both are percentages of the same number, namely  ).
).
Quantity A
The total circumference is calculated using the standard equation:
 or, for our data:
or, for our data: 
Thus, our pertinent percentage is:

Quantity B
For this, the area is computed by the formula:
 or, for our data:
or, for our data: 
Thus, our percentage is:

Clearly,  , so A is larger than B.
, so A is larger than B.
For each of these, you need to compute the total measurement applicable to the given data. For Quantity A, this will be the total circumference. For Quantity B, this will be the total area. You will then divide the given sector calculation by this total amount. By multiplying this percentage by 

Quantity A
The total circumference is calculated using the standard equation:

Thus, our pertinent percentage is:
Quantity B
For this, the area is computed by the formula:

Thus, our percentage is:
Clearly, 
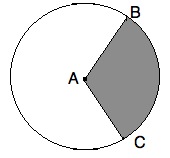
We need to begin by finding the area of the following sector:
If ∠BAC = 120°, then the area of sector BAC is equal to 120 / 360 = 1/3 of the entire circle. Since AC is 12 and is a radius, we know the total area is pi *122 = 144*pi. The sector is then 144*pi / 3 = 48*pi.
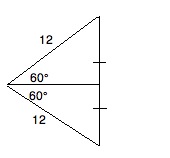
Now, we need to find the area of the triangle ABC. Since AB and AC are equal (both being radii of our circle), we have an icoseles triangle. If we drop a height from ∠BAC, we have the following triangle ABC:
We can use the 30-60-90 rule to find the height and base. One half of the base (x) is found by the following ratio:
√(3) / 2 = x / 12
Solving for x, we get: x = 6 * √(3). Therefore, the base is 12 * √(3).
To find the height (y), we use the following ratio:
1 / 2 = y / 12
Solving for y, we get y = 6.
Therefore, the area of the triangle = 0.5 * 6 * 12 * √(3) = 3 * 12 * √(3) = 36 * √(3)
The area of the shaded region is then 48*pi - 36 * √(3).
We need to begin by finding the area of the following sector:
If ∠BAC = 120°, then the area of sector BAC is equal to 120 / 360 = 1/3 of the entire circle. Since AC is 12 and is a radius, we know the total area is pi *122 = 144*pi. The sector is then 144*pi / 3 = 48*pi.
Now, we need to find the area of the triangle ABC. Since AB and AC are equal (both being radii of our circle), we have an icoseles triangle. If we drop a height from ∠BAC, we have the following triangle ABC:
We can use the 30-60-90 rule to find the height and base. One half of the base (x) is found by the following ratio:
√(3) / 2 = x / 12
Solving for x, we get: x = 6 * √(3). Therefore, the base is 12 * √(3).
To find the height (y), we use the following ratio:
1 / 2 = y / 12
Solving for y, we get y = 6.
Therefore, the area of the triangle = 0.5 * 6 * 12 * √(3) = 3 * 12 * √(3) = 36 * √(3)
The area of the shaded region is then 48*pi - 36 * √(3).
If the outer arc of 1/12th of a circular pie is 7π, what is the area of 1/4th of the pie?
If the outer arc of 1/12th of a circular pie is 7π, what is the area of 1/4th of the pie?
Tap to see back →
Our initial data tells us that (1/12)c = 7π or (1/12)πd = 7π. This simplifies to (1/12)d = 7 or d = 84. Furthermore, we know that r is 42. Given this, we can ascertain the area of a quarter of the whole pie by taking one fourth of the whole area or 0.25 * π * 422 = 0.25 * 1764 * π = 441π
Our initial data tells us that (1/12)c = 7π or (1/12)πd = 7π. This simplifies to (1/12)d = 7 or d = 84. Furthermore, we know that r is 42. Given this, we can ascertain the area of a quarter of the whole pie by taking one fourth of the whole area or 0.25 * π * 422 = 0.25 * 1764 * π = 441π
What is the area of a sector of a circle of radius 4 that spans an arc of 86 degrees?
What is the area of a sector of a circle of radius 4 that spans an arc of 86 degrees?
Tap to see back →
sector area = ∏ * r2 * degrees/360 = ∏ * 42 * 86/360 = 172/45 * ∏
sector area = ∏ * r2 * degrees/360 = ∏ * 42 * 86/360 = 172/45 * ∏
What is the perimeter of a pie piece if the pie is sliced into 40 degree pieces and its area is 361π?
What is the perimeter of a pie piece if the pie is sliced into 40 degree pieces and its area is 361π?
Tap to see back →
The perimeter of a given pie-piece will be equal to 2 radii plus the outer arc (which is a percentage of the circumference). For our piece, this arc will be 40/360 or 1/9 of the circumference. If the area is 361π, this means πr2 = 361 and that the radius is 19. The total circumference is therefore 2 * 19 * π or 38π.
The total perimeter of the pie piece is therefore 2 * r + (1 / 9) * c = 2 * 19 + (1/9) * 38π = 38 + 38π/9
The perimeter of a given pie-piece will be equal to 2 radii plus the outer arc (which is a percentage of the circumference). For our piece, this arc will be 40/360 or 1/9 of the circumference. If the area is 361π, this means πr2 = 361 and that the radius is 19. The total circumference is therefore 2 * 19 * π or 38π.
The total perimeter of the pie piece is therefore 2 * r + (1 / 9) * c = 2 * 19 + (1/9) * 38π = 38 + 38π/9
What is the length of the arc of a circle with radius 10 that traces a 50 degree angle?
What is the length of the arc of a circle with radius 10 that traces a 50 degree angle?
Tap to see back →
length of an arc = (degrees * 2_πr)/360 = (50 * 2_π * 10)/360 = 25_π_/9
length of an arc = (degrees * 2_πr)/360 = (50 * 2_π * 10)/360 = 25_π_/9
An ant walks around the edge of circular pizzas left on the counter of a pizza shop. On most days, it is shaken off the pizza before it manages to walk the complete distance.
Quantity A: The distance covered by the ant when walking over four slices of a pizza with a diameter of  and
and  equally-sized pieces.
equally-sized pieces.
Quantity B: The distance covered by the ant when walking over a complete personal pizza with a diameter of  inches.
inches.
What can we say about the two quantities?
An ant walks around the edge of circular pizzas left on the counter of a pizza shop. On most days, it is shaken off the pizza before it manages to walk the complete distance.
Quantity A: The distance covered by the ant when walking over four slices of a pizza with a diameter of 

Quantity B: The distance covered by the ant when walking over a complete personal pizza with a diameter of 
What can we say about the two quantities?
Tap to see back →
Let's compute each quantity.
Quantity A
This is a little bit more difficult than quantity B. It requires us to compute an arc length, for the ant does not walk around the whole pizza; however, this is not very hard. What we know is that the ant walks around  , or
, or  , of the pizza.
, of the pizza.
Now, we know the circumference of a circle is  or
or 
For our example, let's use the latter. Since  , we know:
, we know:

However, our ant walks around only part of this, namely:

Quantity B
This is really just a matter of computing the circumference of the circle. For our value, we know this to be:

Now, we can compare these by taking quantity A and reducing the fraction to be  . Thus, we know that Quantity B is larger than Quantity A.
. Thus, we know that Quantity B is larger than Quantity A.
Let's compute each quantity.
Quantity A
This is a little bit more difficult than quantity B. It requires us to compute an arc length, for the ant does not walk around the whole pizza; however, this is not very hard. What we know is that the ant walks around 

Now, we know the circumference of a circle is 
For our example, let's use the latter. Since 
However, our ant walks around only part of this, namely:
Quantity B
This is really just a matter of computing the circumference of the circle. For our value, we know this to be:
Now, we can compare these by taking quantity A and reducing the fraction to be 
A given pizza with a  -inch diameter has
-inch diameter has  calories. A baker cuts the pizza using a
calories. A baker cuts the pizza using a  angle for each piece. If Susan eats five such pieces, how many calories does she consume? Round to the nearest calorie.
angle for each piece. If Susan eats five such pieces, how many calories does she consume? Round to the nearest calorie.
A given pizza with a 


Tap to see back →
To solve this, notice that one piece of pizza comprises  of the total pie or (reducing)
of the total pie or (reducing)  of a pie. Now, if Susan buys five slices, she gets:
of a pie. Now, if Susan buys five slices, she gets:
 of the pie. If the complete pie contains
of the pie. If the complete pie contains  calories, she will then eat the following amount of calories:
calories, she will then eat the following amount of calories:

Rounding, this is  calories.
calories.
To solve this, notice that one piece of pizza comprises 



Rounding, this is 
A circle of radius  , for an angle
, for an angle  , has an arc length of
, has an arc length of  . What is the angle
. What is the angle  ?
?

A circle of radius 




Tap to see back →
The formula for an arc length,  , of a circle of a given radius,
, of a circle of a given radius,  , and a given angle,
, and a given angle,  is:
is:

Note that  is the circumference of the circle.
is the circumference of the circle.
Conversely, for a known arc length and unknown angle, this equation can be rewritten as follows:

Plugging in the given values, it is therefore possible to find the missing angle:

The formula for an arc length, 


Note that 
Conversely, for a known arc length and unknown angle, this equation can be rewritten as follows:
Plugging in the given values, it is therefore possible to find the missing angle:
Find the radius of the given circle:

Find the radius of the given circle:

Tap to see back →
To solve this problem, realize that an inscribed angle (an angle formed by two chords) is equal to twice the central angle formed by connecting the origin to the inscribed angle's endpoints:

Now, the formula for an arc length,  , of a circle of a given radius,
, of a circle of a given radius,  , and a given angle,
, and a given angle,  is:
is:

Since the radius is the unknown, this equation can be rewritten as:

Plugging in our values, we find:

To solve this problem, realize that an inscribed angle (an angle formed by two chords) is equal to twice the central angle formed by connecting the origin to the inscribed angle's endpoints:

Now, the formula for an arc length, 


Since the radius is the unknown, this equation can be rewritten as:
Plugging in our values, we find:
An ant begins at the center of a pie with a 12" radius. Walking out to the edge of pie, it then proceeds along the outer edge for a certain distance. At a certain point, it turns back toward the center of the pie and returns to the center point. Its whole trek was 55.3 inches. What is the approximate size of the angle through which it traveled?
An ant begins at the center of a pie with a 12" radius. Walking out to the edge of pie, it then proceeds along the outer edge for a certain distance. At a certain point, it turns back toward the center of the pie and returns to the center point. Its whole trek was 55.3 inches. What is the approximate size of the angle through which it traveled?
Tap to see back →
To solve this, we must ascertain the following:
-
The arc length through which the ant traveled.
-
The percentage of the total circumference in light of that arc length.
-
The percentage of 360° proportionate to that arc percentage.
To begin, let's note that the ant travelled 12 + 12 + x inches, where x is the outer arc distance. (It traveled the radius twice, remember); therefore, we know that 24 + x = 55.3 or x = 31.3.
Now, the total circumference of the circle is 2πr or 24π. The arc is 31.3/24π percent of the total circumference; therefore, the percentage of the angle is 360 * 31.3/24π. Since the answers are approximations, use 3.14 for π. This would be 149.52°.
To solve this, we must ascertain the following:
-
The arc length through which the ant traveled.
-
The percentage of the total circumference in light of that arc length.
-
The percentage of 360° proportionate to that arc percentage.
To begin, let's note that the ant travelled 12 + 12 + x inches, where x is the outer arc distance. (It traveled the radius twice, remember); therefore, we know that 24 + x = 55.3 or x = 31.3.
Now, the total circumference of the circle is 2πr or 24π. The arc is 31.3/24π percent of the total circumference; therefore, the percentage of the angle is 360 * 31.3/24π. Since the answers are approximations, use 3.14 for π. This would be 149.52°.
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.

Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.

Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
Tap to see back →
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
A group of students ate an  -inch pizza that was cut into
-inch pizza that was cut into  equal slices. What was the angle measure needed to cut this pizza into these equal slices?
equal slices. What was the angle measure needed to cut this pizza into these equal slices?
A group of students ate an 

Tap to see back →
You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were  slices. If the slices were evenly divided among the
slices. If the slices were evenly divided among the  degrees of the pizza, this means that the degree measure of each slice was
degrees of the pizza, this means that the degree measure of each slice was  . This reduces to
. This reduces to  degrees.
degrees.
You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were 



John owns 8 black shirts, 7 red shirts, 6 blue shirts and 4 white shirts. If he wants to make a circle chart of his shirts, what is the degree angle corresponding to the "blue shirt section?"
John owns 8 black shirts, 7 red shirts, 6 blue shirts and 4 white shirts. If he wants to make a circle chart of his shirts, what is the degree angle corresponding to the "blue shirt section?"
Tap to see back →
We can set up a ratio to calculate the angle measure as such: 6/25 = x/360, since there are 360 degrees in a circle. Solving, we obtain x = 86.4 degrees.
We can set up a ratio to calculate the angle measure as such: 6/25 = x/360, since there are 360 degrees in a circle. Solving, we obtain x = 86.4 degrees.
A circular pie is cut into 30 pieces. Two people wish to split a piece of the pie, but one person wants to have twice as much as the other person. What is the angle of the smaller piece produced in this manner?
A circular pie is cut into 30 pieces. Two people wish to split a piece of the pie, but one person wants to have twice as much as the other person. What is the angle of the smaller piece produced in this manner?
Tap to see back →
First of all, calculate the angle of each of the full pieces of pie. This is easily found:

Though small, this is what the information tells us! Now, we know that if two people are eating the piece, with one having twice the amount of the other, the angles must be  for the smaller piece and
for the smaller piece and  for the larger one. Thus, we can write the equation:
for the larger one. Thus, we can write the equation:

Simplifying, we get:


That is a tiny piece, but that is what is called for by the data!
First of all, calculate the angle of each of the full pieces of pie. This is easily found:
Though small, this is what the information tells us! Now, we know that if two people are eating the piece, with one having twice the amount of the other, the angles must be 

Simplifying, we get:
That is a tiny piece, but that is what is called for by the data!