Similarity, Right Triangles, & Trigonometry - Geometry
Card 0 of 472
Complete the statement by choosing from one of the following
Regarding the triangle below, to find the area using the formula  , I assume that
, I assume that 

Complete the statement by choosing from one of the following
Regarding the triangle below, to find the area using the formula 


Recall that  for right triangles. When we draw a line down from the vertex to the opposite side this creates two right triangles within the original obtuse triangle. If we are solving for
for right triangles. When we draw a line down from the vertex to the opposite side this creates two right triangles within the original obtuse triangle. If we are solving for  , then
, then  becomes our hypotenuse and
becomes our hypotenuse and  becomes the opposite side we are working with. Therefore
becomes the opposite side we are working with. Therefore  .
.
Recall that 




Compare your answer with the correct one above
Given the triangle below, what is the formula for finding the area?

Given the triangle below, what is the formula for finding the area?

The formula for the area of a triangle is  (base)(height). Since this is an obtuse triangle we need to break it into two right triangles by drawing the line
(base)(height). Since this is an obtuse triangle we need to break it into two right triangles by drawing the line  down from the vertex perpendicular to the opposite side.
down from the vertex perpendicular to the opposite side.
Now that we have two right triangles we can solve for the area of this triangle. Notice our base is 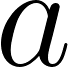 and our height is
and our height is  . Plugging into the formula for the area of a triangle gives us
. Plugging into the formula for the area of a triangle gives us  . Most of the time, we will not have an exact length for
. Most of the time, we will not have an exact length for 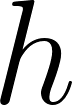 , but we may have, or will be able to solve for, the lengths of
, but we may have, or will be able to solve for, the lengths of  and the angles
and the angles  . Using our
. Using our  relationship for right triangles, we know
relationship for right triangles, we know  . In this case we will use
. In this case we will use  as our angle. So
as our angle. So


We can plug  in for
in for 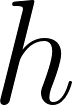 in our formula for area and we are left with
in our formula for area and we are left with  .
.
The formula for the area of a triangle is 
down from the vertex perpendicular to the opposite side.
Now that we have two right triangles we can solve for the area of this triangle. Notice our base is and our height is


, but we may have, or will be able to solve for, the lengths of





We can plug 
in our formula for area and we are left with

Compare your answer with the correct one above
Given the triangle below, find the area and round to the second decimal place (in degrees).

Given the triangle below, find the area and round to the second decimal place (in degrees).


Following from the figure above, we draw an auxiliary line from the vertex perpendicular to the opposite side. We will call this line  for height and will label the new vertex
for height and will label the new vertex  . The formula we will use is
. The formula we will use is  . First we begin by labeling our variables. We will let
. First we begin by labeling our variables. We will let  be the base of our triangle and
be the base of our triangle and  be the hypotenuse of the triangle formed by
be the hypotenuse of the triangle formed by  . The values for the variables are as follows:
. The values for the variables are as follows:



Plugging these into our formula, it follows that:



Following from the figure above, we draw an auxiliary line from the vertex perpendicular to the opposite side. We will call this line 





Plugging these into our formula, it follows that:
Compare your answer with the correct one above
Using the triangle below, find the area then solve for  .
.

Using the triangle below, find the area then solve for 

To solve for  , we first need to find the area using our formula
, we first need to find the area using our formula  , considering the triangle
, considering the triangle  . We will begin by labeling our variables:
. We will begin by labeling our variables:



To find the area, we plug the values for the variables into the formula.


Knowing that our area is 24, we can now solve for  . Recall that:
. Recall that:


It follows that:

 (because
(because  )
)
 (plugging in our values for area and
(plugging in our values for area and  )
)


To solve for 


To find the area, we plug the values for the variables into the formula.
Knowing that our area is 24, we can now solve for 
It follows that:




Compare your answer with the correct one above
Is the following statement True or False?
We want to use the formula  . Consider an obtuse triangle
. Consider an obtuse triangle  . We know the lengths of
. We know the lengths of  and
and  , but only know the angle for
, but only know the angle for  . We are still able to use this formula.
. We are still able to use this formula.
Is the following statement True or False?
We want to use the formula 




There are two approaches to this problem. We are able to calculate the angle  by using the Sine Law. The Sine Law states:
by using the Sine Law. The Sine Law states:

So we can set  and solve accordingly for angle
and solve accordingly for angle  .
.
Our other option is to use the area formula we have been but altering it to correspond to angle  . We would draw our vertical line down from the vertex as shown below and our formula would be in the form
. We would draw our vertical line down from the vertex as shown below and our formula would be in the form  .
.
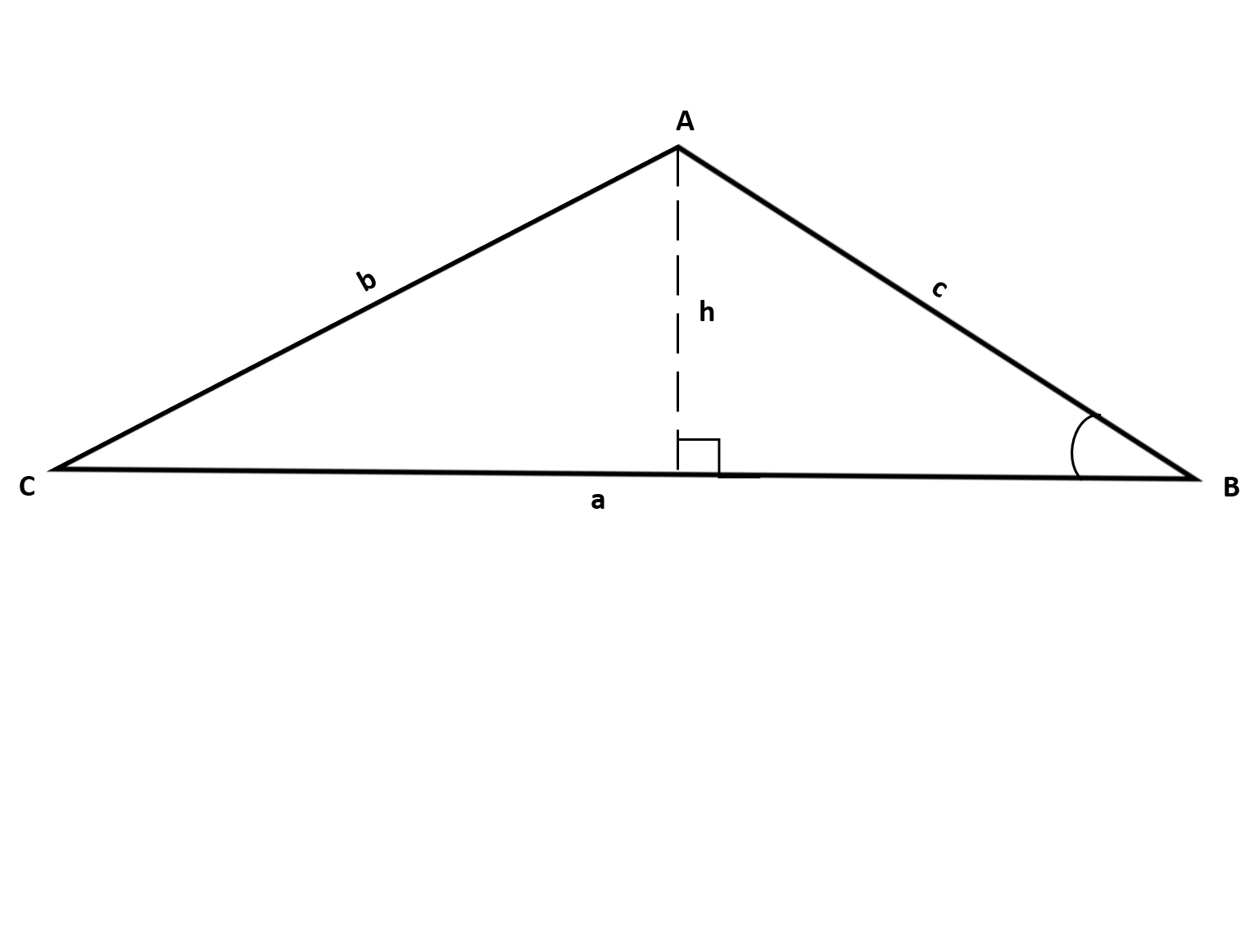
There are two approaches to this problem. We are able to calculate the angle 
So we can set 

Our other option is to use the area formula we have been but altering it to correspond to angle 

Compare your answer with the correct one above
Solve for x using the formula  given that the area of the following triangle is
given that the area of the following triangle is  (round to the second decimal place if needed).
(round to the second decimal place if needed).
Solve for x using the formula 

Even though the formula  is using sides
is using sides  and angle
and angle  , this is a general formula and can be used with any angle in the triangle. Since we are now working with an obtuse angle rather than an acute angle, we need to do some more work to get the logic right.
, this is a general formula and can be used with any angle in the triangle. Since we are now working with an obtuse angle rather than an acute angle, we need to do some more work to get the logic right.

Using the figure above, to be able to label the sides we are using correctly, we extend the original triangle horizontally past the obtuse angle and draw a vertical line down from the top vertex to form a right angle. This vertical line is  . Angle
. Angle  for the supplementary (orange) triangle is
for the supplementary (orange) triangle is  . Using the fact that
. Using the fact that  , we can set up our formula to be the following:
, we can set up our formula to be the following:


 (either
(either  angle can be used and I will show this to be true)
angle can be used and I will show this to be true)

 (Using
(Using 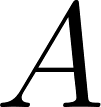 from the original triangle)
from the original triangle)


This shows that when using this formula for an obtuse angle, you can use either the supplementary angle you made, or the original. It is always helpful to draw this supplementary triangle in order to be able to visualize and understand logically how the formula is working for obtuse angles as well.
Even though the formula 


Using the figure above, to be able to label the sides we are using correctly, we extend the original triangle horizontally past the obtuse angle and draw a vertical line down from the top vertex to form a right angle. This vertical line is 




angle can be used and I will show this to be true)

from the original triangle)
This shows that when using this formula for an obtuse angle, you can use either the supplementary angle you made, or the original. It is always helpful to draw this supplementary triangle in order to be able to visualize and understand logically how the formula is working for obtuse angles as well.
Compare your answer with the correct one above
Stephanie is building a triangular garden in her backyard. She has cut wood for the sides with lengths of 5, 4, and 3 feet. Knowing that the height from the vertex $A$ to the base formed by the line $CB$ is 1.778 feet, first find the area that will be in the garden and then calculate each angle that Stephanie will have to put the boards together in order for the lengths to fit just right. Round your answer to the third decimal place if needed.

Stephanie is building a triangular garden in her backyard. She has cut wood for the sides with lengths of 5, 4, and 3 feet. Knowing that the height from the vertex $A$ to the base formed by the line $CB$ is 1.778 feet, first find the area that will be in the garden and then calculate each angle that Stephanie will have to put the boards together in order for the lengths to fit just right. Round your answer to the third decimal place if needed.

We must begin by finding the area first. To find the area we begin by using our equation  and recall that
and recall that  . We will let:
. We will let:







So our area is 
How to find  :
:  ,
,  ,
, 







How to find  :
:  ,
,  ,
, 






To find  , we know the angles of a triangle should add up to 180 so:
, we know the angles of a triangle should add up to 180 so:



We must begin by finding the area first. To find the area we begin by using our equation 

So our area is
How to find 


How to find 


To find 
Compare your answer with the correct one above
Is the following statement True or False?
In order to use this formula, you only need to know two of the triangles sides' lengths.
Is the following statement True or False?
In order to use this formula, you only need to know two of the triangles sides' lengths.
In order to use this formula you need to either the height (which can be used to find the angle) or the angle (which can be used to find the height).
In order to use this formula you need to either the height (which can be used to find the angle) or the angle (which can be used to find the height).
Compare your answer with the correct one above
Using the information from the following triangle, find the area. Round to the second decimal place.

Using the information from the following triangle, find the area. Round to the second decimal place.

Using the formula  , we will let
, we will let  and
and 



Using the formula 

Compare your answer with the correct one above
You are making your friend a triangular fabric decoration for their home. It has ripped so you need to go buy new fabric. The fabric you are buying is \$3 per square foot. Using the dimensions below, how much money do you need to buy enough fabric?

You are making your friend a triangular fabric decoration for their home. It has ripped so you need to go buy new fabric. The fabric you are buying is \$3 per square foot. Using the dimensions below, how much money do you need to buy enough fabric?

Using the formula  , we will let
, we will let  and
and  .
.

 (because
(because  )
)


Then we must account for each square foot costing \$3.

The answer is \$162.
Using the formula 




Then we must account for each square foot costing \$3.
The answer is \$162.
Compare your answer with the correct one above
The Law of Cosines is a generalization of which common theorem?
The Law of Cosines is a generalization of which common theorem?
The Law of Cosines is a generalization of the Pythagorean Theorem. To better understand this, start by drawing triangle ABC with sides a, b, and c. Then, construct the altitude from point A to get height h. Finally label the distance between point B and the point where h meets side a as distance r.

We will arbitrarily work to solve for side b, but we could do the same for a and c (after drawing the correct altitudes), which is why we can generalize that the other two formulas to find a and c follow.
By definition, we know that  . If we multiply both sides by c, we get
. If we multiply both sides by c, we get  .
.
Also, we know that  . If we multiply both sides by c, we get
. If we multiply both sides by c, we get  .
.
Using the Pythagorean Theorem, we get  .
.
Substituting in h and r from above, we get:


 (because
(because  )
)

Therefore  .
.
The other two versions of Law of Cosines are:


The Law of Cosines is a generalization of the Pythagorean Theorem. To better understand this, start by drawing triangle ABC with sides a, b, and c. Then, construct the altitude from point A to get height h. Finally label the distance between point B and the point where h meets side a as distance r.

We will arbitrarily work to solve for side b, but we could do the same for a and c (after drawing the correct altitudes), which is why we can generalize that the other two formulas to find a and c follow.
By definition, we know that 

Also, we know that 

Using the Pythagorean Theorem, we get 
Substituting in h and r from above, we get:


Therefore 
The other two versions of Law of Cosines are:
Compare your answer with the correct one above
Choose the answer choice that correctly states the Law of Sines, given the triangle below.

Choose the answer choice that correctly states the Law of Sines, given the triangle below.

The Law of Sines uses ratios of a triangle’s sides and angles to allow us to be able to solve for unknown sides and/or angles. This relationship is true for any triangle.

The Law of Sines is  .
.
The Law of Sines uses ratios of a triangle’s sides and angles to allow us to be able to solve for unknown sides and/or angles. This relationship is true for any triangle.

The Law of Sines is 
Compare your answer with the correct one above
Which of the following expressions correctly states the Law of Cosines? Use the following triangle for reference.

Which of the following expressions correctly states the Law of Cosines? Use the following triangle for reference.

The Law of Cosines should look similar to a theorem we use quite commonly for right triangles. The Law of Cosines is basically the Pythagorean Theorem, but it has an added argument so that it is true for any and all triangles.

The Law of Cosines is 
The Law of Cosines should look similar to a theorem we use quite commonly for right triangles. The Law of Cosines is basically the Pythagorean Theorem, but it has an added argument so that it is true for any and all triangles.

The Law of Cosines is
Compare your answer with the correct one above
Choose the answer choice that correctly states the Law of Sines, given the triangle below.

Choose the answer choice that correctly states the Law of Sines, given the triangle below.

The Law of Sines uses ratios of a triangle’s sides and angles to allow us to be able to solve for unknown sides and/or angles. This relationship is true for any triangle.

The Law of Sines is  .
.
The Law of Sines uses ratios of a triangle’s sides and angles to allow us to be able to solve for unknown sides and/or angles. This relationship is true for any triangle.

The Law of Sines is 
Compare your answer with the correct one above
True or false: The Law of Sines applies to all types of triangles.
True or false: The Law of Sines applies to all types of triangles.
This is true. While the Pythagorean Theorem only applies to right triangles, the Law of Sines applies to all triangles no matter if they are right, acute, or obtuse.
This is true. While the Pythagorean Theorem only applies to right triangles, the Law of Sines applies to all triangles no matter if they are right, acute, or obtuse.
Compare your answer with the correct one above
True or False: The Law of Cosines applies to all triangles.
True or False: The Law of Cosines applies to all triangles.
This is true. While the Pythagorean Theorem only applies to right triangles, the Law of Cosines applies to all triangles no matter if they are right, acute, or obtuse.
This is true. While the Pythagorean Theorem only applies to right triangles, the Law of Cosines applies to all triangles no matter if they are right, acute, or obtuse.
Compare your answer with the correct one above
Assume the following two triangles are similar. Using the fact that their side ratios are  , what trigonomic function could this represent for angles
, what trigonomic function could this represent for angles  and
and  ?
?

Assume the following two triangles are similar. Using the fact that their side ratios are 



We must begin by manipulating our equation of the side ratios to get fractions that include both of the sides of the same triangles:


If we look at angle  , we see that
, we see that  is the
is the  . Looking at angle
. Looking at angle  we see that
we see that  is also the
is also the  . This is the definition of the sine function. So:
. This is the definition of the sine function. So:

We must begin by manipulating our equation of the side ratios to get fractions that include both of the sides of the same triangles:
If we look at angle 





Compare your answer with the correct one above
Using the information of the side lengths in the triangle below, use the side ratios to find the  .
.

Using the information of the side lengths in the triangle below, use the side ratios to find the 

The definition of cosine of an acute angle is  . So here we must determine what sides are adjacent and which is the hypotenuse. The hypotenuse is the easiest to pick out. This is the side that is directly across from the right angle in a right triangle. Our hypotenuse is
. So here we must determine what sides are adjacent and which is the hypotenuse. The hypotenuse is the easiest to pick out. This is the side that is directly across from the right angle in a right triangle. Our hypotenuse is 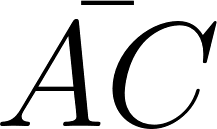 . Now we must choose the adjacent side. Adjacent means next to, and since
. Now we must choose the adjacent side. Adjacent means next to, and since  is our hypotenuse then
is our hypotenuse then  must be our adjacent side. So:
must be our adjacent side. So:



The definition of cosine of an acute angle is 
. Now we must choose the adjacent side. Adjacent means next to, and since


Compare your answer with the correct one above
Assume the two triangles below are similar. Using the fact that their sides ratios are  , what trigonometric function could this represent for angles
, what trigonometric function could this represent for angles  and
and 

Assume the two triangles below are similar. Using the fact that their sides ratios are 


We must begin by manipulating our equation of the side ratios to get fractions that include both of the sides of the same triangles:

 multiply both sides by
multiply both sides by 
 divide both sides by
divide both sides by 
If we look at angle  we see that
we see that  is the
is the  . Looking at angle
. Looking at angle  we see that
we see that  is also
is also  . This is the definition of the cosine function of an angle. So:
. This is the definition of the cosine function of an angle. So:

We must begin by manipulating our equation of the side ratios to get fractions that include both of the sides of the same triangles:


If we look at angle 





Compare your answer with the correct one above
Using the sides of a right triangle, what is the definition of  ?
?
Using the sides of a right triangle, what is the definition of 
We can see this to be true by looking at the following triangle.
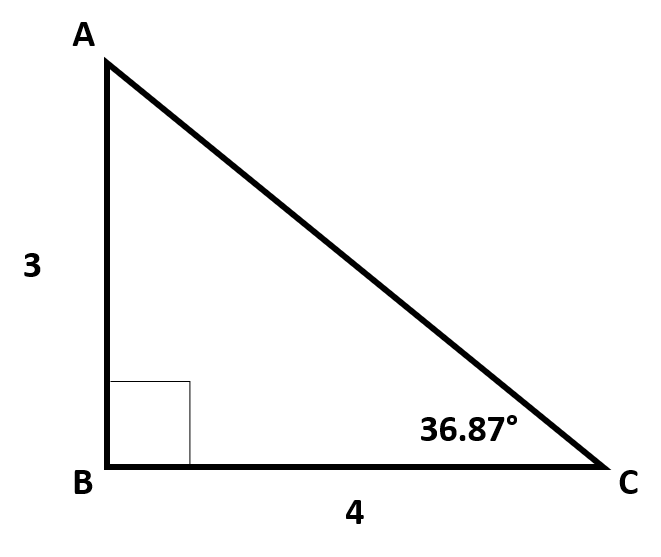
We are considering  . The opposite side to
. The opposite side to  is
is  .
.  has two adjacent sides, but since
has two adjacent sides, but since  is opposite to the right angle, this is the hypotenuse of the triangle. So the adjacent side to
is opposite to the right angle, this is the hypotenuse of the triangle. So the adjacent side to  must be
must be  . We can set up the following equation to check and make sure that
. We can set up the following equation to check and make sure that  .
.



This shows that  .
.
We can see this to be true by looking at the following triangle.
We are considering 







This shows that 
Compare your answer with the correct one above












































































