How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem - Geometry
Card 0 of 440
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
Compare your answer with the correct one above
Which of the following sets of sides cannnot belong to a right triangle?
Which of the following sets of sides cannnot belong to a right triangle?
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
Compare your answer with the correct one above
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
Compare your answer with the correct one above
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = _x_2
9 + 16 = _x_2
25 = _x_2
5 = x
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = _x_2
9 + 16 = _x_2
25 = _x_2
5 = x
Compare your answer with the correct one above
Which set of side lengths CANNOT correspond to a right triangle?
Which set of side lengths CANNOT correspond to a right triangle?
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Compare your answer with the correct one above
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
Compare your answer with the correct one above
What is the hypotenuse of a right triangle with sides 5 and 8?
What is the hypotenuse of a right triangle with sides 5 and 8?
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Compare your answer with the correct one above
A right triangle has side lengths of 21 and 72. What is the length of the hypotenuse?
A right triangle has side lengths of 21 and 72. What is the length of the hypotenuse?
By the Pythagorean Theorem, 212 + 722 = hyp2. Then hyp2 = 5625, and the hypotenuse = 75. If you didn't know how to figure out that 752 = 5625, that's okay. Look at the answer choices. We could easily have squared them and chosen the answer choice that, when squared, equals 5625.
By the Pythagorean Theorem, 212 + 722 = hyp2. Then hyp2 = 5625, and the hypotenuse = 75. If you didn't know how to figure out that 752 = 5625, that's okay. Look at the answer choices. We could easily have squared them and chosen the answer choice that, when squared, equals 5625.
Compare your answer with the correct one above
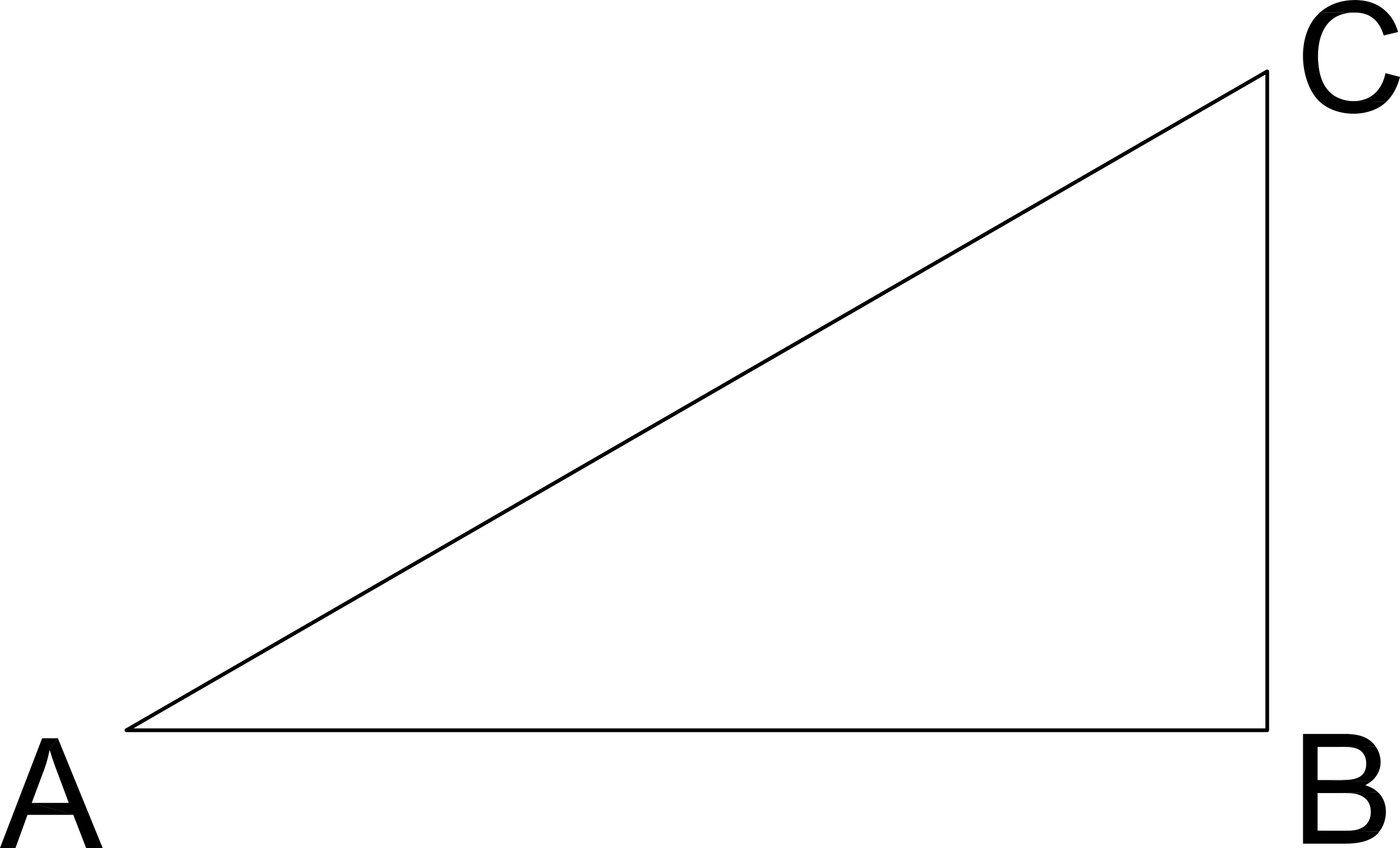
Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?
Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: _AB_2 + _BC_2 = _AC_2
42 + 32 = _AC_2
16 + 9 = _AC_2
25 = _AC_2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: _AB_2 + _BC_2 = _AC_2
42 + 32 = _AC_2
16 + 9 = _AC_2
25 = _AC_2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Compare your answer with the correct one above
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Compare your answer with the correct one above
In the figure above, 
is a square and 
is three times the length of 
. What is the area of 
?
In the figure above,
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
Compare your answer with the correct one above
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Compare your answer with the correct one above
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
Compare your answer with the correct one above
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Compare your answer with the correct one above
The lengths of the sides of a triangle are consecutive odd numbers and the triangle's perimeter is 57 centimeters. What is the length, in centimeters, of its longest side?
The lengths of the sides of a triangle are consecutive odd numbers and the triangle's perimeter is 57 centimeters. What is the length, in centimeters, of its longest side?
First, define the sides of the triangle. Because the side lengths are consecutive odd numbers, if we define the shortest side will be as 
, the next side will be defined as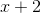 
, and the longest side will be defined as 
. We can then find the perimeter of a triangle using the following formula:
Substitute in the known values and variables.
Subtract 6 from both sides of the equation.
Divide both sides of the equation by 3.
Solve.
This is not the answer; we need to find the length of the longest side, or 
.
Substitute in the calculated value for 
and solve.
The longest side of the triangle is 21 centimeters long.
First, define the sides of the triangle. Because the side lengths are consecutive odd numbers, if we define the shortest side will be as 
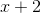
Substitute in the known values and variables.
Subtract 6 from both sides of the equation.
Divide both sides of the equation by 3.
Solve.
This is not the answer; we need to find the length of the longest side, or 
Substitute in the calculated value for 
The longest side of the triangle is 21 centimeters long.
Compare your answer with the correct one above
Angela drives 30 miles north and then 40 miles east. How far is she from where she began?
Angela drives 30 miles north and then 40 miles east. How far is she from where she began?
By drawing Angela’s route, we can connect her end point and her start point with a straight line and will then have a right triangle. The Pythagorean theorem can be used to solve for how far she is from the starting point: a2+b2=c2, 302+402=c2, c=50. It can also be noted that Angela’s route represents a multiple of the 3-4-5 Pythagorean triple.
By drawing Angela’s route, we can connect her end point and her start point with a straight line and will then have a right triangle. The Pythagorean theorem can be used to solve for how far she is from the starting point: a2+b2=c2, 302+402=c2, c=50. It can also be noted that Angela’s route represents a multiple of the 3-4-5 Pythagorean triple.
Compare your answer with the correct one above
An airplane is 8 miles west and 15 miles south of its destination. Approximately how far is the plane from its destination, in miles?
An airplane is 8 miles west and 15 miles south of its destination. Approximately how far is the plane from its destination, in miles?
A right triangle can be drawn between the airplane and its destination.
Destination
15 miles 
Airplane
8 miles
We can solve for the hypotenuse, x, of the triangle:
82 + 152 = x2
64 + 225 = x2
289 = x2
x = 17 miles
A right triangle can be drawn between the airplane and its destination.
Destination
15 miles Airplane
8 miles
We can solve for the hypotenuse, x, of the triangle:
82 + 152 = x2
64 + 225 = x2
289 = x2
x = 17 miles
Compare your answer with the correct one above
The lengths of the sides of a right triangle are consecutive integers, and the length of the shortest side is 
. Which of the following expressions could be used to solve for 
?
The lengths of the sides of a right triangle are consecutive integers, and the length of the shortest side is
Since the lengths of the sides are consecutive integers and the shortest side is 
, the three sides are 
, 
, and 
.
We then use the Pythagorean Theorem:
Since the lengths of the sides are consecutive integers and the shortest side is
We then use the Pythagorean Theorem:
Compare your answer with the correct one above
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
cannot be the side lengths of a right triangle. 
does not equal 
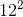. Also, special right triangle 
and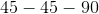 
rules can eliminate all the other choices.
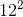
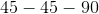
Compare your answer with the correct one above
The height of a right circular cylinder is 10 inches and the diameter of its base is 6 inches. What is the distance from a point on the edge of the base to the center of the entire cylinder?
The height of a right circular cylinder is 10 inches and the diameter of its base is 6 inches. What is the distance from a point on the edge of the base to the center of the entire cylinder?
The best thing to do here is to draw diagram and draw the appropiate triangle for what is being asked. It does not matter where you place your point on the base because any point will produce the same result. We know that the center of the base of the cylinder is 3 inches away from the base (6/2). We also know that the center of the cylinder is 5 inches from the base of the cylinder (10/2). So we have a right triangle with a height of 5 inches and a base of 3 inches. So using the Pythagorean Theorem 32 + 52 = c2. 34 = c2, c = √(34).
The best thing to do here is to draw diagram and draw the appropiate triangle for what is being asked. It does not matter where you place your point on the base because any point will produce the same result. We know that the center of the base of the cylinder is 3 inches away from the base (6/2). We also know that the center of the cylinder is 5 inches from the base of the cylinder (10/2). So we have a right triangle with a height of 5 inches and a base of 3 inches. So using the Pythagorean Theorem 32 + 52 = c2. 34 = c2, c = √(34).
Compare your answer with the correct one above