How to find out if lines are parallel - Geometry

Card 0 of 76

Question

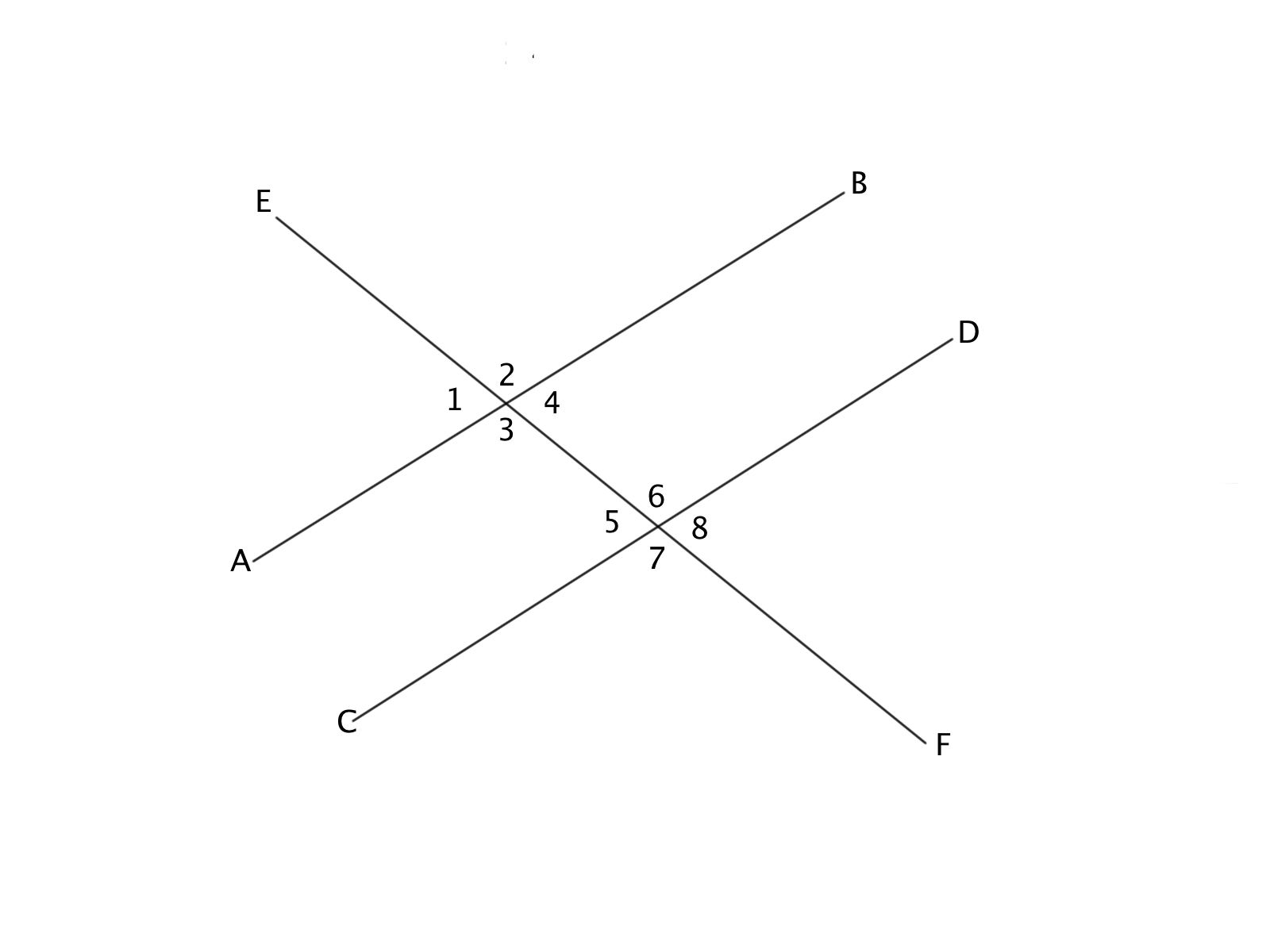
If lines AB and CD are parallel, angles 2 and 7 are congruent based on which theorem?

Answer

Angles 2 and 7 are both on the exterior side of the transverse, this means they are Alternate Exterior Angles.

Compare your answer with the correct one above

Question

If lines AB and CD are parallel, which angles are congruent to Angle 3?

Answer

Angle 2 is congruent based on the Vertical Angle Theorem. Angle 7 is congruent based on the Corresponding Angles Theorem. Angle 6 is congruent based on the Alternate Interior Angles theorem.

Compare your answer with the correct one above

Question

Where do the lines and intersect.

Answer

By solving both equations to standard form , you can see that both lines have the same slope, and therefore will never intersect.

Compare your answer with the correct one above

Question

A line passes through both the coordinates and . A line passing through which other pair of coodinates would be parallel to this line?

Answer

The line has a slope of $-\frac{4}{3}$ , so you must find a pair of points which has the same slope.

Compare your answer with the correct one above

Question

Angles 2 and 3 are congruent based on which Theorem?

Answer

Veritcal angles means that the angles share the same vertex. Angles 2 and 3 are a vertical pair of angles, which mean that they are congruent.

Compare your answer with the correct one above

Question

If angles 2 and 6 are congruent, lines AB and CD are parallel based on which theorem?

Answer

Angles 2 and 6 are Corresponding Angles. If each of the set of angles were taken separately, angels 2 and 6 would occupy the same place and are thus corresponding angles.

Compare your answer with the correct one above

Question

What is the sum of Angle 3 and Angle 5?

Answer

Because of the Consecutive Interior Angle theorem, the sum of Angles 3 and 5 would be 180 deg.

Compare your answer with the correct one above

Question

If lines AB and CD are parallel, angles 1 and 8 are congruent based on which theorem?

Answer

Angles 1 and 8 are on the exterior of the parallel lines and are on opposite sides of the transversal. This means the Theorem is the Alternate Exterior Angle theorem.

Compare your answer with the correct one above

Question

If Angles 2 and 7 are congruent, line AB and CD are __________.

Answer

Lines AB and CD are parallel based on the Alternate Exterior Angle theorem.

Compare your answer with the correct one above

Question

If lines AB and CD are parallel, angles 5 and 1 are __________.

Answer

If the two lines are parallel, the transverse line makes it so that angles 2 and 7 are corresponding angles.

Compare your answer with the correct one above

Question

If lines AB and CD are parallel, the sum of Angle 6 plus Ange 4 equals __________.

Answer

If lines AB and CD are parallel, the sum of Angles 4 and 6 is 180 deg based on the Consecutive Interior Angle Theorem.

Compare your answer with the correct one above

Question

Which answer contains all the angles (other than itself) that are congruent to Angle 1?

Answer

Because of the Corresponding Angles Theorem (Angle 2 and Angle 5), Alternate Exterior Angles (Angle 2 and Angle 8), and Vertical Angles (Angle 2 and Angle 4).

Compare your answer with the correct one above

Question

A line which includes the point is parallel to the line with equation

Which of these points is on that line?

Answer

Write the given equation in slope-intercept form:

$\frac{1}{2}\cdot 2y=\frac{1}{2}\cdot \left (-4x \right )+\frac{1}{2}\cdot 15$

$y=-2x+\frac{15}{2}$

The given line has slope , so this is the slope of any line parallel to that line.

We can use the slope formula $m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ , testing each of our choices.

$(9, -2):; m = \frac{4-(-2)}{6-9}}=\frac{6}{-3}=-2$

$(10, 6):; m = \frac{4-6}{6-10}}=\frac{-2}{-4}=\frac{1}{2}$

$(5,2):; m = \frac{4-2}{6-5}}=\frac{2}{1}=2$

$(6,2):; m = \frac{4-2}{6-6}}=\frac{2}{0}$ , which is undefined

$(0, 7):; m = \frac{4-7}{6-0}}=\frac{-3}{6}=-\frac{1}{2}$

The only point whose inclusion yields a line with slope is .

Compare your answer with the correct one above

Question

Choose the equation that represents a line that is parallel to .

Answer

Two lines are parallel if and only if they have the same slope. To find the slopes, we must put the equations into slope-intercept form, , where equals the slope of the line. In this case, we are looking for . To put into slope-intercept form, we must subtract from each side of the equation, giving us . We then subtract from each side, giving us . Finally, we divide both sides by , giving us , which is parallel to .

Compare your answer with the correct one above

Question

Which of the following lines are parallel?

Answer

None of these lines are parallel.

In order for lines to be parallel, the lines must NEVER cross. Lines with identical slopes never cross. An example of two parallel lines would be:

Note that only the slope determines if line are parallel.

Compare your answer with the correct one above

Question

Are the lines of the equations

$y = \frac{1}{2} x + 7$

and

parallel, perpendicular, or neither?

Answer

Write each equation in the slope-intercept form by solving for ; the -coefficient is the slope of the line.

The first equation,

$y = \frac{1}{2} x + 7$ ,

is in the slope-intercept form form. The slope is the -coefficient $\frac{1}{2}$ .

is not in this form, so it should be rewritten as such by multiplying both sides by $\frac{1}{2}$ :

$\frac{1}{2} \cdot 2y =\frac{1}{2} \cdot ( x + 7)$

$y =\frac{1}{2} \cdot x + \frac{1}{2} \cdot 7$

$y =\frac{1}{2} x + \frac{7}{2}$

The slope of the line of this equation is the -coefficient $\frac{1}{2}$ .

The lines of both equations have the same slope, $\frac{1}{2}$ , so it follows that they are parallel.

Compare your answer with the correct one above

Question

One line on the coordinate plane has its intercepts at and . A second line has its intercepts at and . Are the lines parallel, perpendicular, or neither?

Answer

To answer this question, we must determine the slopes of both lines. If a line has as its intercepts and , its slope is

$m = -\frac{b}{a}$

The first line has as its slope

$m = -\frac{4}{7}$

The second line has as its slope

$m = -\frac{7}{-4} = \frac{7}{4}$

Two lines are parallel if and only if their slopes are equal; this is not the case.

They are perpendicular if and only if the product of their slopes is . The product of the slopes of the given lines is

$-\frac{4}{7} \cdot \frac{7}{4} = -1$ ,

so they are perpendicular.

Compare your answer with the correct one above

Question

The slopes of two lines on the coordinate plane are 0.333 and $\frac{1}{3}$ .

True or false: the lines are parallel.

Answer

Two lines are parallel if and only if they have the same slope. The slope of one of the lines is 0.333. The other line has slope $\frac{1}{3}$ , which is equal to ; this is not equal to 0.333. The two lines are not parallel.

Compare your answer with the correct one above

Question

The slopes of two lines on the coordinate plane are 0.75 and $\frac{3}{4}$ .

True or false: The lines are parallel.

Answer

Two lines are parallel if and only if they have the same slope. The slope of one of the lines is $0.75 = \frac{75}{100}= \frac{3}{4}$ . The slope of the other is $\frac{3}{4}$ , so the lines have the same slope. The lines are parallel.

Compare your answer with the correct one above

Question

If lines AB and CD are parallel, angles 2 and 7 are congruent based on which theorem?

Answer

Angles 2 and 7 are both on the exterior side of the transverse, this means they are Alternate Exterior Angles.

Compare your answer with the correct one above

Tap the card to reveal the answer