Transformation - Geometry
Card 0 of 96
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
Tap to see back →
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
Regular pentagons have lines of symmetry through each vertex and the center of the opposite side, meaning the y-axis forms a line of symmetry in this instance. Therefore, point P is negative b units in the x-direction, and c units in the y-direction. It is a reflection of point (b,c) across the y-axis.
Regular pentagons have lines of symmetry through each vertex and the center of the opposite side, meaning the y-axis forms a line of symmetry in this instance. Therefore, point P is negative b units in the x-direction, and c units in the y-direction. It is a reflection of point (b,c) across the y-axis.
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
Tap to see back →
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.
Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.
Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
Tap to see back →
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
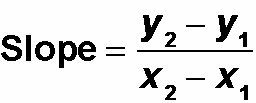
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
What is the period of the function?
What is the period of the function?
Tap to see back →
The period is the time it takes for the graph to complete one cycle.
In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches 
.
Therefore, the period is 
The period is the time it takes for the graph to complete one cycle.
In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches
Therefore, the period is
If this is a sine graph, what is the phase displacement?
If this is a sine graph, what is the phase displacement?
Tap to see back →
The phase displacement is the shift from the center of the graph. Since this is a sine graph and the sin(0) = 0, this is in phase.
The phase displacement is the shift from the center of the graph. Since this is a sine graph and the sin(0) = 0, this is in phase.
If this is a cosine graph, what is the phase displacement?
If this is a cosine graph, what is the phase displacement?
Tap to see back →
The phase displacement is the shift of the graph. Since cos(0) = 1, the phase shift is π because the graph is at its high point then.
The phase displacement is the shift of the graph. Since cos(0) = 1, the phase shift is π because the graph is at its high point then.
If g(x) is a transformation of f(x) that moves the graph of f(x) four units up and three units left, what is g(x) in relation to f(x)?
If g(x) is a transformation of f(x) that moves the graph of f(x) four units up and three units left, what is g(x) in relation to f(x)?
Tap to see back →
To solve this question, you must have an understanding of standard transformations. To move a function along the x-axis in the positive direction, you must subtract the value from the operative x-value. For example, to move a function, f(x), five units to the left would be f(x+5).
To shift a function along the y-axis in the positive direction, you must add the value to the overall function. For example, to move a function, f(x), three units up would be f(x)+3.
The question asks us to move the function, f(x), left three units and up four units. f(x+3) will move the function three units to the left and f(x)+4 will move it four units up.
Together, this gives our final answer of f(x+3)+4.
To solve this question, you must have an understanding of standard transformations. To move a function along the x-axis in the positive direction, you must subtract the value from the operative x-value. For example, to move a function, f(x), five units to the left would be f(x+5).
To shift a function along the y-axis in the positive direction, you must add the value to the overall function. For example, to move a function, f(x), three units up would be f(x)+3.
The question asks us to move the function, f(x), left three units and up four units. f(x+3) will move the function three units to the left and f(x)+4 will move it four units up.
Together, this gives our final answer of f(x+3)+4.
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
Tap to see back →
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
The graphs of f(x) and g(x) are shown above. Which equation best describes the relationship between f(x) and g(x)?
The graphs of f(x) and g(x) are shown above. Which equation best describes the relationship between f(x) and g(x)?
Tap to see back →
If the point (6, 7) is reflected over the line y=x and then over the x-axis, what is the resulting coordinate?
If the point (6, 7) is reflected over the line y=x and then over the x-axis, what is the resulting coordinate?
Tap to see back →
A reflection over the line y=x involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
A reflection over the line y=x involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
Tap to see back →
The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:
The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so
The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:
The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so
Let 
. If 
is equal to 
when flipped across the x-axis, what is the equation for 
?
Let
Tap to see back →
When a function 
is flipped across the x-axis, the new function 
is equal to 
. Therefore, our function 
is equal to:
Our final answer is therefore 
When a function
Our final answer is therefore
Let 
. If we let 
equal 
when it is flipped across the y-axis, what is the equation for 
?
Let
Tap to see back →
When a function 
is flipped across the y-axis, the resulting function 
is equal to 
. Therefore, to find our 
, we must substitute in 
for every 
is our equation:
Our final answer is therefore 
When a function
Our final answer is therefore
Let 
. If 
represents 
is shifted 
places to the right and 
places upwards, what is the equation for 
?
Let
Tap to see back →
When a function 
is transformed 
units upwards, the new function 
is equal to 
. Likewise, if 
is transformed 
units to the right, the new function 
is equal to 
. Therfore, we can first find the upwards transformation by adding 
to the function:
Now we can apply the horizontal transformation by replacing all 
's in the function with 
. Our transformed function therefore becomes:
We then multiply this out to obtain:
Our final answer is therefore 
When a function
Now we can apply the horizontal transformation by replacing all
We then multiply this out to obtain:
Our final answer is therefore
Assume we have a triangle, 
, with the following vertices:
, 
, and 
If 
were reflected across the line 
, what would be the coordinates of the new vertices?
Assume we have a triangle, 
If 
Tap to see back →
When we reflect a point across the line, 
, we swap the x- and y-coordinates; therefore, in each point, we will switch the x and y-coordinates:
becomes 
,
becomes 
, and
becomes 
.
The correct answer is the following:
The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.
When we reflect a point across the line, 
The correct answer is the following:
The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.
How is 
different from 
?
How is
Tap to see back →
The standard form of a linear equation is 
Here, we are given two equations, 
and 
, which differ only in their 
terms. In other words, these functions differ only in their slope. 
has a larger slope than does 
, so 
is steeper.
The standard form of a linear equation is
Given 
, write an equation 
that represents a vertical shift four units upward.
Given
Tap to see back →
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 
. Changes to the slope (
) will make the graph steeper or shallower, changes to the y-intercept (
) will shift the graph vertically, and changes to the indepent variable (
) will shift the graph horizontally. Here, we are given 
and asked to transform it into a new equation vertically shifted up four units. We can accomplish this by adding four to the constant term, so the correct answer is 
.
multiples the slope by four, which will result in a steeper graph.
subtracts four from the constant term, which shifts the graph vertically, but in the wrong direction.
adds four to the independent variable, which shifts the graph horizontally to the left.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is
Given 
, write an equation that represents a horizontal shift two units to the right.
Given
Tap to see back →
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is . Changes to the slope () will make the graph steeper or shallower, changes to the y-intercept () will shift the graph vertically, and changes to the indepent variable () will shift the graph horizontally. Here, we are given 
and asked to transform it into a new equation horizontally shifted to the right two units. We can accomplish this by subtracting two from the independent variable, so the correct answer is 
.
adds two to the constant term, which shifts the graph vertically.
adds two to the independent variable which shifts the graph horizontally, but in the wrong direction.
multiplies the slope by two, which makes the graph steeper.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is
Given 
, write an equation that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
Given
Tap to see back →
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is . Changes to the slope () will make the graph steeper or shallower, changes to the y-intercept () will shift the graph vertically, and changes to the indepent variable () will shift the graph horizontally. Here, we are given 
and asked to transform it into a new equation that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
First, multiply the slope by three.
Add one to the independent variable.
Subtract three from the constant term.
correctly increases the slope and subtracts three from the constant term, but fails to properly substitute 
for 
, leading to an erroneous simplification. In other words, 
becomes 
.
shifts the function to the right instead of the left.
shifts the function both right and up, rather than left and down.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is
First, multiply the slope by three.
Add one to the independent variable.
Subtract three from the constant term.