Statistics - GED Math
Card 0 of 1320
The grade a student earns for a course depends on the mean of the best four of the five tests he takes. The minimum mean score for each grade is as follows:
A: 90
B: 80
C: 70
D: 60
Charles earned 68, 50, 77, 73, and 80 on his five tests. What was his letter grade?
The grade a student earns for a course depends on the mean of the best four of the five tests he takes. The minimum mean score for each grade is as follows:
A: 90
B: 80
C: 70
D: 60
Charles earned 68, 50, 77, 73, and 80 on his five tests. What was his letter grade?
Tap to see back →
Charlie's lowest score was a 50, so his grade was the mean of 68, 77, 73, and 80, which is the sum of the scores divided by the number of scores, 4;
,
so Charlie made a grade of "C".
Charlie's lowest score was a 50, so his grade was the mean of 68, 77, 73, and 80, which is the sum of the scores divided by the number of scores, 4;
so Charlie made a grade of "C".
A penny is altered so that the odds are 5 to 4 against it coming up tails when tossed; a nickel is altered so that the odds are 4 to 3 against it coming up tails when tossed. If both coins are tossed, what are the odds of there being two heads or two tails?
A penny is altered so that the odds are 5 to 4 against it coming up tails when tossed; a nickel is altered so that the odds are 4 to 3 against it coming up tails when tossed. If both coins are tossed, what are the odds of there being two heads or two tails?
Tap to see back →
5 to 4 odds in favor of heads is equal to a probability of 
, which is the probability that the penny will come up heads. The probability that the penny will come up tails is 
.
Similarly, 4 to 3 odds in favor of heads is equal to a probability of 
, which is the probability that the nickel will come up heads. The probablity that the nickel will come up tails is 
.
The outcomes of the tosses of the penny and the nickel are independent, so the probabilities can be multiplied.
The probability of the penny and the nickel both coming up heads is 
.
The probability of the penny and the nickel both coming up tails is 
.
The probabilities are added:
Since 
, this translates to 32 to 31 odds in favor of this event.
5 to 4 odds in favor of heads is equal to a probability of
Similarly, 4 to 3 odds in favor of heads is equal to a probability of
The outcomes of the tosses of the penny and the nickel are independent, so the probabilities can be multiplied.
The probability of the penny and the nickel both coming up heads is
The probability of the penny and the nickel both coming up tails is
The probabilities are added:
Since
The above bar graph compares exit examination scores from both 2012 and 2013 for the five high schools in a school district.
Which school saw the most improvement in its median math score between 2012 and 2013?
The above bar graph compares exit examination scores from both 2012 and 2013 for the five high schools in a school district.
Which school saw the most improvement in its median math score between 2012 and 2013?
Tap to see back →
Wallace, Gerry, and Burr all saw improvement, as the bars representing their 2013 median scores are longer than the ones for 2012. A visual inspection shows that the greatest difference is between the two bars representing Wallace High, so Wallace is the correct choice.
Wallace, Gerry, and Burr all saw improvement, as the bars representing their 2013 median scores are longer than the ones for 2012. A visual inspection shows that the greatest difference is between the two bars representing Wallace High, so Wallace is the correct choice.
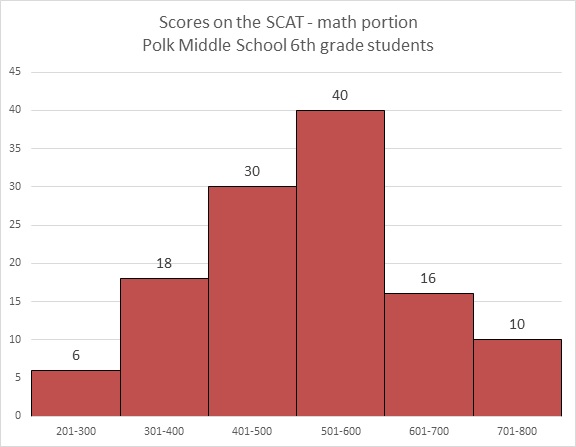
Refer to the above bar graph.
How many students at Polk Middle School scored higher than 600 on the math portion of the SCAT?
Refer to the above bar graph.
How many students at Polk Middle School scored higher than 600 on the math portion of the SCAT?
Tap to see back →
The number of students who scored in the 601-700 range is 16; in the 701-800 range, 10. Add them to get 26 students total.
The number of students who scored in the 601-700 range is 16; in the 701-800 range, 10. Add them to get 26 students total.
Which question can be answered about Polk Middle School sixth graders' performance on the math portion of the SCAT by looking at the above bar graph?
Which question can be answered about Polk Middle School sixth graders' performance on the math portion of the SCAT by looking at the above bar graph?
Tap to see back →
The graph only provides information about how many students scored in each range (201-300, 301-400, etc.) on the test; it provides no information about the mean, median, or mode. The only question that can be answered is the number of students total who took the test - this can be answered by adding the numbers on top of the bars.
The graph only provides information about how many students scored in each range (201-300, 301-400, etc.) on the test; it provides no information about the mean, median, or mode. The only question that can be answered is the number of students total who took the test - this can be answered by adding the numbers on top of the bars.
Which question cannot be answered about Polk Middle School sixth graders' performance on the math portion of the SCAT by looking at the above bar graph?
Which question cannot be answered about Polk Middle School sixth graders' performance on the math portion of the SCAT by looking at the above bar graph?
Tap to see back →
The lowest score is not indicated anywhere on the graph, so the question "What was the lowest score on the test?" is the one that cannot be answered. The other three can be determined, in part or completely, by adding the number of students in one or more ranges, and in two cases, also adding the number of students total.
The lowest score is not indicated anywhere on the graph, so the question "What was the lowest score on the test?" is the one that cannot be answered. The other three can be determined, in part or completely, by adding the number of students in one or more ranges, and in two cases, also adding the number of students total.
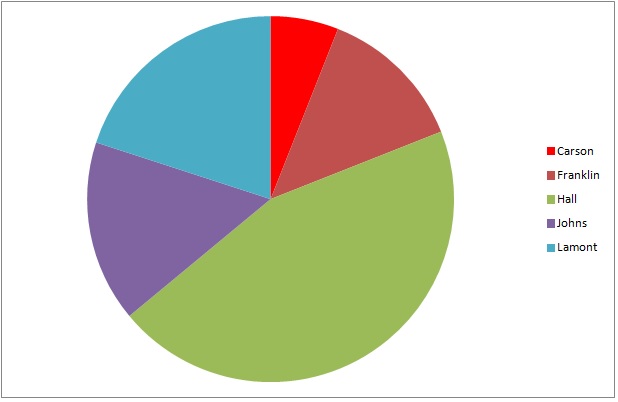
The above represents the results of a student council election at Jefferson High. According to the results, the top three finishers will be awarded seats on the student council.
Which two did not win a seat on the student council?
The above represents the results of a student council election at Jefferson High. According to the results, the top three finishers will be awarded seats on the student council.
Which two did not win a seat on the student council?
Tap to see back →
The wedges, in descending order by size, are those representing Hall, Lamont, Johns, Franklin, Carson. Hall, Lamont, and Johns were elected to the student council, so the correct choice is Franklin and Carson.
The wedges, in descending order by size, are those representing Hall, Lamont, Johns, Franklin, Carson. Hall, Lamont, and Johns were elected to the student council, so the correct choice is Franklin and Carson.
Veronica went to the mall and bought several gifts for her sister's birthday. The prices of the items were the following:
$8, $10, $6, $7, $10, $2, $5, $3, $4
What is the medianprice of the gifts?
Veronica went to the mall and bought several gifts for her sister's birthday. The prices of the items were the following:
$8, $10, $6, $7, $10, $2, $5, $3, $4
What is the medianprice of the gifts?
Tap to see back →
To find the median, first reorder the prices in ascending order:
$2, $3, $4, $5, $6, $7, $8, $10, $10
The median is the middle number in a data set.
Here, the middle number in this set of nine prices is the 5th number, which is $6.
$2, $3, $4, $5, $6, $7, $8, $10, $10
To find the median, first reorder the prices in ascending order:
$2, $3, $4, $5, $6, $7, $8, $10, $10
The median is the middle number in a data set.
Here, the middle number in this set of nine prices is the 5th number, which is $6.
$2, $3, $4, $5, $6, $7, $8, $10, $10
Philip went to a family reunion this weekend and met his extended cousins, whose ages were the following:
10, 21, 7, 8, 19, 20, 8, 15, 17, and 13.
What is the medianage?
Philip went to a family reunion this weekend and met his extended cousins, whose ages were the following:
10, 21, 7, 8, 19, 20, 8, 15, 17, and 13.
What is the medianage?
Tap to see back →
The median is the middlenumber in a data set.
To find the median, rearrange the numbers in ascending order and find the middle number:
Given: 10, 21, 7, 8, 19, 20, 8, 15, 17, 13.
In order: 7, 8, 8, 10, 13, 15, 17, 19, 20, 21.
Since the data set has 10 numbers, which is even, the median is the average of the two middle numbers. The two numbers in the middle of this data set are 13 and 15. Their average, or the number in between them, is 14.
Therefore the median age is 14.
The median is the middlenumber in a data set.
To find the median, rearrange the numbers in ascending order and find the middle number:
Given: 10, 21, 7, 8, 19, 20, 8, 15, 17, 13.
In order: 7, 8, 8, 10, 13, 15, 17, 19, 20, 21.
Since the data set has 10 numbers, which is even, the median is the average of the two middle numbers. The two numbers in the middle of this data set are 13 and 15. Their average, or the number in between them, is 14.
Therefore the median age is 14.
Calculate the mean of the following numbers:
Calculate the mean of the following numbers:
Tap to see back →
Find the mean of the following numbers:
Find the mean of the following numbers:
Tap to see back →
Find the mean of the set of numbers below:
Find the mean of the set of numbers below:
Tap to see back →
In this list, 
In this list,
John would like to have a 90 average for math for this semester. John received a 78, 89, 100 on three of his tests. What is the lowest grade he could receive on his last test in order for him to get a 90 average for the semester?
John would like to have a 90 average for math for this semester. John received a 78, 89, 100 on three of his tests. What is the lowest grade he could receive on his last test in order for him to get a 90 average for the semester?
Tap to see back →
In order for John to maintain a 90 average for the marking period, his total for four tests must be 360.
or 
If you add up the scores that he already received, he already has 267 points.
If you take the total of 267, which is the total amount of points for the three tests already taken and subtract it from the 360 points which is the total amount of points needed for a 90 average, he would need to get a 93 on his last test.
In order for John to maintain a 90 average for the marking period, his total for four tests must be 360.
If you add up the scores that he already received, he already has 267 points.
If you take the total of 267, which is the total amount of points for the three tests already taken and subtract it from the 360 points which is the total amount of points needed for a 90 average, he would need to get a 93 on his last test.
Veronica scored a 75 and a 71 on her first two exams. To raise her mean score to an 80, what grade does she need to earn on her third test?
Veronica scored a 75 and a 71 on her first two exams. To raise her mean score to an 80, what grade does she need to earn on her third test?
Tap to see back →
The mean score is the sum of all scores divided by the number of scores.
First, find the sum of all three test scores, then divide by the number of tests, 3.
If Veronica wants her average to be 80, the equation becomes:
We need to solve for 
.
First, multiply both sides of the equation by 3:
Subtract 146 from both sides:
Veronica must score a 94 on her third test in order to bring her mean score to 80.
The mean score is the sum of all scores divided by the number of scores.
First, find the sum of all three test scores, then divide by the number of tests, 3.
If Veronica wants her average to be 80, the equation becomes:
We need to solve for
First, multiply both sides of the equation by 3:
Subtract 146 from both sides:
Veronica must score a 94 on her third test in order to bring her mean score to 80.
Veronica went to the mall and bought several small gifts for her sister's birthday. The prices of the items were the following:
$8, $10, $6, $3, $7, $10, $2, $5, $3
What is the mean price?
Veronica went to the mall and bought several small gifts for her sister's birthday. The prices of the items were the following:
$8, $10, $6, $3, $7, $10, $2, $5, $3
What is the mean price?
Tap to see back →
The meanof a set is the sum of all elements divided by the number of elements in the set:
The mean is $6.
The meanof a set is the sum of all elements divided by the number of elements in the set:
The mean is $6.
On the first two tests of the year, James scored 100 and 70, respectively. He then scored a 96 on his third test. There is just one test remaining, and James wants to finish the semester with a 90 average. What score does he need to receive on the fourth test of the semester to finish with a mean score of 90?
On the first two tests of the year, James scored 100 and 70, respectively. He then scored a 96 on his third test. There is just one test remaining, and James wants to finish the semester with a 90 average. What score does he need to receive on the fourth test of the semester to finish with a mean score of 90?
Tap to see back →
The meanin a data set of scores is the sum of all scores divided by the number of scores:
Call the fourth test score 
. Plug in what we know and solve for 
:
Multiply both sides by 4:
Then, subtract 266 from both sides:.
To finish with a mean of 90, James must score a 94 on his fourth test.
The meanin a data set of scores is the sum of all scores divided by the number of scores:
Call the fourth test score
Multiply both sides by 4:
Then, subtract 266 from both sides:.
To finish with a mean of 90, James must score a 94 on his fourth test.
Determine the mean of the numbers: 
Determine the mean of the numbers:
Tap to see back →
The mean is the average of all the numbers in the set of data.
Add the numbers together and divide the sum by 4.
The answer is: 
The mean is the average of all the numbers in the set of data.
Add the numbers together and divide the sum by 4.
The answer is:
Determine the mean of the numbers: 
Determine the mean of the numbers:
Tap to see back →
The mean is the average of all the number ins the data set.
Add all the numbers and divide the sum by four.
The answer is: 
The mean is the average of all the number ins the data set.
Add all the numbers and divide the sum by four.
The answer is:
Use the following data set of test scores to answer the question:
Find the mean.
Use the following data set of test scores to answer the question:
Find the mean.
Tap to see back →
To find the mean (or average), we will use the following formula:
So, given the set
we can calculate the following:
We can also calculate the following:
because there are 7 numbers in the data set.
So, we can substitute. We get
Therefore, the mean of the data set is 86.
To find the mean (or average), we will use the following formula:
So, given the set
we can calculate the following:
We can also calculate the following:
because there are 7 numbers in the data set.
So, we can substitute. We get
Therefore, the mean of the data set is 86.
A Science class took an exam. Here are the scores of 9 students:
Find the mean score.
A Science class took an exam. Here are the scores of 9 students:
Find the mean score.
Tap to see back →
To find the mean, we will use the following formula:
Now, given the set
We can calculate the following:
We can also calculate the following:
because if we count, we can see there are 9 numbers in the set.
So, we can substitute. We get
Therefore, the mean score is 84.
To find the mean, we will use the following formula:
Now, given the set
We can calculate the following:
We can also calculate the following:
because if we count, we can see there are 9 numbers in the set.
So, we can substitute. We get
Therefore, the mean score is 84.