Other Shapes - GED Math
Card 0 of 190
Give the number of sides of a regular polygon whose interior angles have measure 
.
Give the number of sides of a regular polygon whose interior angles have measure
Tap to see back →
The easiest way to solve this is to look at the exterior angles, each of which have measure 
. Since each exterior angle of a regular polygon with 
sides is 
, we solve for 
in the following equation:
The polygon has 36 sides.
The easiest way to solve this is to look at the exterior angles, each of which have measure
The polygon has 36 sides.
What is the measure of each angle of a regular octagon?
What is the measure of each angle of a regular octagon?
Tap to see back →
The sum of the degree measures of the angles of a polygon with 
sides is 
. Since an octagon has eight sides, substitute 
to get:
Each angle of a regular polygon has equal measure, so divide this by 8 to get the measure of one angle:
, the degree measure of one angle.
The sum of the degree measures of the angles of a polygon with
Each angle of a regular polygon has equal measure, so divide this by 8 to get the measure of one angle:
Give the measure of each interior angle of a regular 72-sided polygon.
Give the measure of each interior angle of a regular 72-sided polygon.
Tap to see back →
A regular polygon with 
sides has interior angles of measure 
each. Substitute 72 for 
.
A regular polygon with
Note: Figure NOT drawn to scale.
The above hexagon is regular. What is 
?
Note: Figure NOT drawn to scale.
The above hexagon is regular. What is
Tap to see back →
Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures
.
The four angles of the quadrilateral are 
. Their sum is 
, so we can set up an equation and solve for 
:
Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures
The four angles of the quadrilateral are
The above octagon is regular. What is 
?
The above octagon is regular. What is
Tap to see back →
Three of the angles of the pentagon formed are angles of a regular octagon, so each measures
.
The five angles of the pentagon are 
. Their sum is 
, so we can set up an equation and solve for 
:
Three of the angles of the pentagon formed are angles of a regular octagon, so each measures
The five angles of the pentagon are
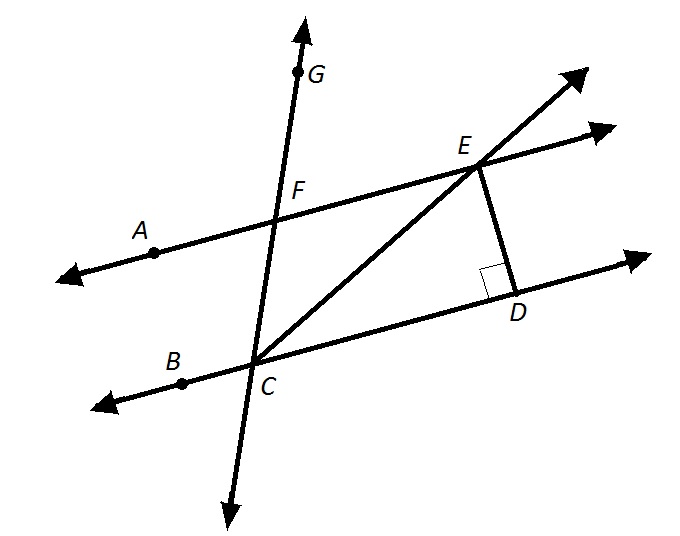
Refer to the above diagram.
Which of these is a valid alternative name for 
?
Refer to the above diagram.
Which of these is a valid alternative name for
Tap to see back →
When naming an angle after three points, the middle letter must be its vertex, or the point at which its sides meet - this is 
. The other two letters must refer to points on its two sides. Therefore, 
includes 
on one side, making one of its sides 
, and 
on the other, making the other side 
.
An alternative name for this angle must be one of two things:
It can be named only after its vertex - that is, 
- but only if there is no ambiguity as to which angle is being named. Since more than one angle in the diagram has vertex 
, 
is not a correct choice.
It can be named after three points. Again, the middle letter must be vertex 
, so we can throw out 
and 
.
The only possible choice is 
.
When naming an angle after three points, the middle letter must be its vertex, or the point at which its sides meet - this is
An alternative name for this angle must be one of two things:
It can be named only after its vertex - that is,
It can be named after three points. Again, the middle letter must be vertex
The only possible choice is
Refer to the above figure. 
is equilateral, and Quadrilateral 
is a square.
Evaluate 
.
Refer to the above figure.
Evaluate
Tap to see back →
By angle addition,
.
, as an angle of an equilateral triangle, has measure 
.
, as an angle of a square, has measure 
.
Therefore,
.
By angle addition,
Therefore,
Refer to the above figure, which shows Square 
and regular Pentagon 
.
Evaluate 
.
Refer to the above figure, which shows Square
Evaluate
Tap to see back →
By angle addition,
.
is an angle of a regular pentagon and has measure 
.
is one of two acute angles of isosceles right triangle 
, so 
.
By angle addition,
Note: Figure NOT drawn to scale.
Refer to the above figure. 
is equilateral and Pentagon 
is regular.
Evaluate 
.
Note: Figure NOT drawn to scale.
Refer to the above figure.
Evaluate
Tap to see back →
First, we find 
.
By angle addition,
.
is an angle of a regular pentagon and has measure 
.
, as an angle of an equilateral triangle, has measure .
is equilateral, so 
; Pentagon 
is regular, so 
. Therefore, 
, and by the Isosceles Triangle Theorem, 
.
The degree measures of three angles of a triangle total 
, so:
First, we find
By angle addition,
The degree measures of three angles of a triangle total
Three consecutive even angles add up to 
. What must be the value of the second largest angle?
Three consecutive even angles add up to
Tap to see back →
Let 
be an even angle. The next consecutive even values are 
.
Set up an equation such that all angles added equal to 180.
Divide by three on both sides.
The second largest angle is 
.
Substitute the value of 
in to the expression.
The answer is: 
Let
Set up an equation such that all angles added equal to 180.
Divide by three on both sides.
The second largest angle is
Substitute the value of
The answer is:
Note: Figure NOT drawn to scale.
Refer to the above diagram. 
. 
is a right angle. What percent of 
has been shaded in?
Note: Figure NOT drawn to scale.
Refer to the above diagram.
Tap to see back →
is a right triangle with legs 
; its area is half the product of its legs, which is
is a right triangle with legs
and
;
its area is half the product of its legs, which is
The shaded region is the former triangle removed from the latter triangle; its area is the difference of the two: 
.
This region is therefore
of 
.
and
its area is half the product of its legs, which is
The shaded region is the former triangle removed from the latter triangle; its area is the difference of the two:
This region is therefore
Note: Figure NOT drawn to scale.
Refer to the above diagram. 
. 
is a right angle. What is the area of the shaded region?
Note: Figure NOT drawn to scale.
Refer to the above diagram.
Tap to see back →
is a right triangle with legs 
; its area is half the product of its legs, which is
is a right triangle with legs
and
;
its area is half the product of its legs, which is
The shaded region is the former triangle removed from the latter triangle; its area is the difference of the two: 
.
and
its area is half the product of its legs, which is
The shaded region is the former triangle removed from the latter triangle; its area is the difference of the two:
The above hexagon is regular. Give its area.
The above hexagon is regular. Give its area.
Tap to see back →
A regular hexagon can be divided into six triangles, each of which can be easily proved equilateral, as seen in the diagram below:
All segments shown are congruent, and, since the diameter shown in the original diagram is 4, each sidelength is half this, or 2.
Each equilateral triangle has area
.
There are six such triangles, so the total area of the hexagon is six times this, or 
.
A regular hexagon can be divided into six triangles, each of which can be easily proved equilateral, as seen in the diagram below:
All segments shown are congruent, and, since the diameter shown in the original diagram is 4, each sidelength is half this, or 2.
Each equilateral triangle has area
There are six such triangles, so the total area of the hexagon is six times this, or
Give the area of a regular hexagon with perimeter 36.
Give the area of a regular hexagon with perimeter 36.
Tap to see back →
A hexagon has six sides; a regular hexagon with perimeter 36 has sidelength
.
A regular hexagon can be divided into six triangles, each of which can be easily proved equilateral, as seen in the diagram below:
Each equilateral triangle has sidelength 6, so each has area
.
The total area of the hexagon is the area of six such triangles:
A hexagon has six sides; a regular hexagon with perimeter 36 has sidelength
A regular hexagon can be divided into six triangles, each of which can be easily proved equilateral, as seen in the diagram below:
Each equilateral triangle has sidelength 6, so each has area
The total area of the hexagon is the area of six such triangles:
Determine the area of a square with a side length of 
.
Determine the area of a square with a side length of
Tap to see back →
Write the area of a square.
Substitute the side into the formula.
The answer is: 
Write the area of a square.
Substitute the side into the formula.
The answer is:
Figure NOT drawn to scale.
Refer to the above figure. Every angle shown is a right angle.
Give its area.
Figure NOT drawn to scale.
Refer to the above figure. Every angle shown is a right angle.
Give its area.
Tap to see back →
Examine the bottom figure, in which the bottom two sides have been connected. Note that the figure is now a rectangle cut out of a rectangle, and, since the opposite sides of a rectangle have the same length, we can fill in some of the side lengths as shown:
The figure is a 60-by-40 rectangle cut from a 100-by-100 square, so, to get the area of the figure, subtract the area of the former from that of the latter. The area of a rectangle is equal to the product of its dimensions, so the areas of the rectangle and the square are, respectively,
and
,
making the area of the figure
.
Examine the bottom figure, in which the bottom two sides have been connected. Note that the figure is now a rectangle cut out of a rectangle, and, since the opposite sides of a rectangle have the same length, we can fill in some of the side lengths as shown:
The figure is a 60-by-40 rectangle cut from a 100-by-100 square, so, to get the area of the figure, subtract the area of the former from that of the latter. The area of a rectangle is equal to the product of its dimensions, so the areas of the rectangle and the square are, respectively,
and
making the area of the figure
A circle is inscribed in square that has a side length of 
, as shown by the figure below.
Find the area of the shaded region. Use 
.
A circle is inscribed in square that has a side length of
Find the area of the shaded region. Use
Tap to see back →
Since the circle is inscribed in the square, the diameter of the circle is the same length as the length of a square.
Start by finding the area of the square.
For the given square,
Now, because the diameter of the circle is the same as the length of a side of the square, we now also know that the radius of the circle must be 
. Next recall how to find the area of a circle.
Plug in the found radius to find the area of the circle.
Now, the shaded area is the area left over when the area of the circle is subtracted from the area of the square. Thus, we can write the following equation to find the area of the shaded region.
Since the circle is inscribed in the square, the diameter of the circle is the same length as the length of a square.
Start by finding the area of the square.
For the given square,
Now, because the diameter of the circle is the same as the length of a side of the square, we now also know that the radius of the circle must be
Plug in the found radius to find the area of the circle.
Now, the shaded area is the area left over when the area of the circle is subtracted from the area of the square. Thus, we can write the following equation to find the area of the shaded region.
Josh wants to build a circular pool in his square yard that measures 
feet on each side. He wants to build the pool as big as possible, then pave the rest of his yard in tile. In square feet, what is the area of the yard that will be tiled? Round your answer to the nearest tenths place.
Josh wants to build a circular pool in his square yard that measures
Tap to see back →
Start by drawing out the square yard and the circular pool in a way that maximizes the area of the pool.
Notice that the diameter of the pool will be the same length as the side of the square.
Since the question asks about the area that is left over after the pool is built, we can find that area by subtracting the area of the pool from the area of the square.
Start by finding the area of the square.
Next, find the area of the circular pool.
Since the diameter of the pool is 
, the radius of the pool must be 
. Recall how to find the area of a circle:
Plug in the radius of the circle.
Subtract the area of the circle from that of the square.
Start by drawing out the square yard and the circular pool in a way that maximizes the area of the pool.
Notice that the diameter of the pool will be the same length as the side of the square.
Since the question asks about the area that is left over after the pool is built, we can find that area by subtracting the area of the pool from the area of the square.
Start by finding the area of the square.
Next, find the area of the circular pool.
Since the diameter of the pool is
Plug in the radius of the circle.
Subtract the area of the circle from that of the square.
The above figure is a regular octagon. Give its perimeter in yards.
The above figure is a regular octagon. Give its perimeter in yards.
Tap to see back →
A regular octagon has eight sides of equal length, so multiply the length of one side by eight:
feet.
Divide by three to get the equivalent in yards:
yards.
A regular octagon has eight sides of equal length, so multiply the length of one side by eight:
Divide by three to get the equivalent in yards:
Identify the above polygon.
Identify the above polygon.
Tap to see back →
A polygon with eight sides is called an octagon.
A polygon with eight sides is called an octagon.