Transforms of Periodic Functions - Differential Equations
Card 0 of 4
Find the Laplace transform of the periodic function.

Find the Laplace transform of the periodic function.
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
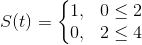
it has a period of
 .
.
and furthermore,

Using the Transform of a Periodic Function Theorem which states,
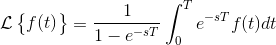
the problem can be solved as follows.

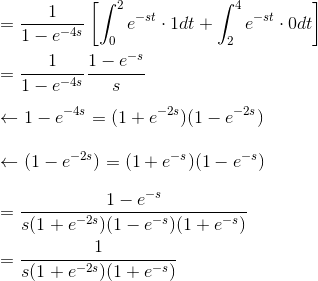
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
it has a period of

and furthermore,
Using the Transform of a Periodic Function Theorem which states,
the problem can be solved as follows.
Compare your answer with the correct one above
Find the Laplace transform of the periodic function.

Find the Laplace transform of the periodic function.
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
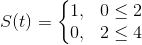
it has a period of
 .
.
and furthermore,

Using the Transform of a Periodic Function Theorem which states,
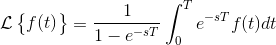
the problem can be solved as follows.

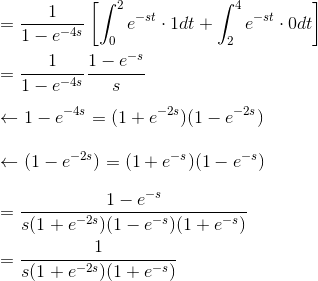
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
it has a period of

and furthermore,
Using the Transform of a Periodic Function Theorem which states,
the problem can be solved as follows.
Compare your answer with the correct one above
Find the Laplace transform of the periodic function.

Find the Laplace transform of the periodic function.
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
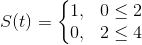
it has a period of
 .
.
and furthermore,

Using the Transform of a Periodic Function Theorem which states,
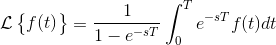
the problem can be solved as follows.

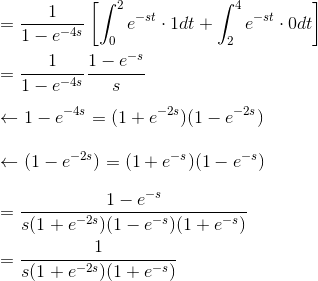
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
it has a period of

and furthermore,
Using the Transform of a Periodic Function Theorem which states,
the problem can be solved as follows.
Compare your answer with the correct one above
Find the Laplace transform of the periodic function.

Find the Laplace transform of the periodic function.
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
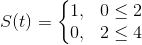
it has a period of
 .
.
and furthermore,

Using the Transform of a Periodic Function Theorem which states,
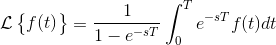
the problem can be solved as follows.

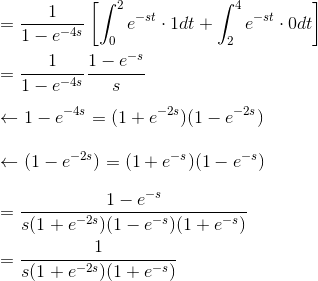
This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.
For this particular function
it has a period of

and furthermore,
Using the Transform of a Periodic Function Theorem which states,
the problem can be solved as follows.
Compare your answer with the correct one above