Modeling Higher-Order Differential Equations - Differential Equations
Card 0 of 4
For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to see back →
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 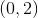
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to see back →
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 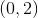
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to see back →
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 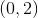
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to see back →
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 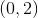
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where
