Higher-Order Differential Equations - Differential Equations
Card 0 of 80
Solve the initial value problem  for
for  and
and  .
.
Solve the initial value problem 


Tap to see back →
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to see back →
This differential equation has characteristic equation of:
 It must be noted that this characteristic equation has a double rootof r=5.
It must be noted that this characteristic equation has a double rootof r=5.
Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is
 in the case of a repeated root such as this,
in the case of a repeated root such as this,  and is the repeated root r=5.
and is the repeated root r=5.
Therefore, the solution is

This differential equation has characteristic equation of:

Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is


Therefore, the solution is
Solve the initial value problem  for
for  and
and 
Solve the initial value problem 

Tap to see back →
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that (Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
(Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
Find the general solution to  .
.
Find the general solution to 
Tap to see back →
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.
To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see


Which tells us the the polynomial factors into  and that
and that  . This means that the fundamental set of solutions is
. This means that the fundamental set of solutions is 
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . As this is not an initial value problem and just asks for the general solution, we are done.
. As this is not an initial value problem and just asks for the general solution, we are done.
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see
Which tells us the the polynomial factors into 

As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to see back →
The ode has a characteristic equation of  .
.
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.
 (for real repeated roots)
(for real repeated roots)
Thus, the solution is,

The ode has a characteristic equation of 
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.

Thus, the solution is,
Solve the General form of the differential equation:

Solve the General form of the differential equation:
Tap to see back →
This differential equation has a characteristic equation of
 , which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:
, which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:

with r being the roots of the characteristic equation.
Thus, the solution is

This differential equation has a characteristic equation of

with r being the roots of the characteristic equation.
Thus, the solution is
Solve the general homogeneous part of the following differential equation:

Solve the general homogeneous part of the following differential equation:
Tap to see back →
We start off by noting that the homogeneous equation we are trying to solve is given as
 .
.
This differential equation thus has characteristic equation of
 .
.
This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:

We start off by noting that the homogeneous equation we are trying to solve is given as

This differential equation thus has characteristic equation of

This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:
Find a general solution to the following Differential Equation

Find a general solution to the following Differential Equation
Tap to see back →
Solving the auxiliary equation

Trying out candidates for roots from the Rational Root Theorem we have a root  .
.
Factoring completely we have

Our general solution is

where  are arbitrary constants.
are arbitrary constants.
Solving the auxiliary equation
Trying out candidates for roots from the Rational Root Theorem we have a root 
Factoring completely we have
Our general solution is
where 
For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to see back →
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 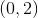
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

Solve the given differential equation by undetermined coefficients.

Solve the given differential equation by undetermined coefficients.
Tap to see back →
First solve the homogeneous portion:

Therefore,  is a repeated root thus one of the complimentary solutions
is a repeated root thus one of the complimentary solutions  is,
is,

Now find the remaining complimentary solution  .
.

Now solve for  and
and  .
.

Where

and

Therefore,

Now, combine both of the complimentary solutions together to arrive at the general solution.

First solve the homogeneous portion:
Therefore, 

Now find the remaining complimentary solution 
Now solve for 

Where
and
Therefore,
Now, combine both of the complimentary solutions together to arrive at the general solution.
Find the general solution for  .
.
Find the general solution for 
Tap to see back →
This is a higher order inhomogeneous linear differential equation. Because the inhomogeneity is a cosine, we will use variation of parameters to solve it.
First, we find the characteristic equation to solve for the homogenous solution. This gives us  .
.
This tells us that the homogeneous solution is  . As neither of these overlap with our inhomogeneity, we are safe to continue without adding a factor of t.
. As neither of these overlap with our inhomogeneity, we are safe to continue without adding a factor of t.
Thus, let us guess that  . Then,
. Then,
 and
and

Plugging into the original equation, we have

Which implies that  and
and  . Solving via substitution,
. Solving via substitution,



Thus, the particular solution is  and the overall solution is the particular plus the homogeneous.
and the overall solution is the particular plus the homogeneous.
So

This is a higher order inhomogeneous linear differential equation. Because the inhomogeneity is a cosine, we will use variation of parameters to solve it.
First, we find the characteristic equation to solve for the homogenous solution. This gives us 
This tells us that the homogeneous solution is 
Thus, let us guess that 

Plugging into the original equation, we have
Which implies that 

Thus, the particular solution is 
So
Find the form of a particular solution to the following differential equation that could be used in the method of undetermined coefficients:

Find the form of a particular solution to the following differential equation that could be used in the method of undetermined coefficients:
Tap to see back →
We first note that the differential equation has characteristic equation
 ,
,
since the roots of this characteristic polynomial are linearly independent of the forcing function
 ,
,
we simply use undetermined coefficient combination rules to figure that the particular solution will be of form

We first note that the differential equation has characteristic equation

since the roots of this characteristic polynomial are linearly independent of the forcing function

we simply use undetermined coefficient combination rules to figure that the particular solution will be of form
Consider the differential equation

The particular solution used in undetermined coefficients will be of what form?
Consider the differential equation
The particular solution used in undetermined coefficients will be of what form?
Tap to see back →
We first figure that the forcing function  is linearly independent to the homogeneous solution solved with the characteristic equation.
is linearly independent to the homogeneous solution solved with the characteristic equation.
Therefore, using proper undetermined coefficients function rules, the particular solution will be of the form:

It is important to note that when either a sine or a cosine is used, both sine and cosine must show up in the particular solution guess.
We first figure that the forcing function 
Therefore, using proper undetermined coefficients function rules, the particular solution will be of the form:
It is important to note that when either a sine or a cosine is used, both sine and cosine must show up in the particular solution guess.
Solve for a particular solution of the differential equation using the method of undetermined coefficients.

Solve for a particular solution of the differential equation using the method of undetermined coefficients.
Tap to see back →
We start with the assumption that the particular solution must be of the form
 .
.
Then we solve the first and second derivatives with this assumption, that is,
 and
and  .
.
Then we plug in these quantities into the given equation to get:
 , which solves for
, which solves for  .
.
Thus, but the method of undetermined coefficients, a particular solution to this differential equation is:

We start with the assumption that the particular solution must be of the form

Then we solve the first and second derivatives with this assumption, that is,


Then we plug in these quantities into the given equation to get:


Thus, but the method of undetermined coefficients, a particular solution to this differential equation is:
Solve the given differential equation by undetermined coefficients.

Solve the given differential equation by undetermined coefficients.
Tap to see back →
First solve the homogeneous portion:

Therefore,  is a repeated root thus one of the complimentary solutions
is a repeated root thus one of the complimentary solutions  is,
is,

Now find the remaining complimentary solution  .
.

Now solve for  and
and  .
.

Where

and

Therefore,

Now, combine both of the complimentary solutions together to arrive at the general solution.

First solve the homogeneous portion:
Therefore, 

Now find the remaining complimentary solution 
Now solve for 

Where
and
Therefore,
Now, combine both of the complimentary solutions together to arrive at the general solution.
Find the form of a particular solution to the following Differential Equation (Do NOT Solve)

Find the form of a particular solution to the following Differential Equation (Do NOT Solve)
Tap to see back →
The form of a guess for a particular solution is

The form of a guess for a particular solution is
Using Variation of Parameters compute the Wronskian of the following equation.

Using Variation of Parameters compute the Wronskian of the following equation.
Tap to see back →
To compute the Wronskian first calculates the roots of the homogeneous portion.


Therefore one of the complimentary solutions is in the form,

where,

Next compute the Wronskian:

Now take the determinant to finish calculating the Wronskian.

To compute the Wronskian first calculates the roots of the homogeneous portion.
Therefore one of the complimentary solutions is in the form,
where,
Next compute the Wronskian:
Now take the determinant to finish calculating the Wronskian.
Using Variation of Parameters compute the Wronskian of the following equation.

Using Variation of Parameters compute the Wronskian of the following equation.
Tap to see back →
To compute the Wronskian first calculates the roots of the homogeneous portion.


Therefore one of the complimentary solutions is in the form,

where,

Next compute the Wronskian:

Now take the determinant to finish calculating the Wronskian.

To compute the Wronskian first calculates the roots of the homogeneous portion.
Therefore one of the complimentary solutions is in the form,
where,
Next compute the Wronskian:
Now take the determinant to finish calculating the Wronskian.
Solve the following non-homogeneous differential equation. 
Solve the following non-homogeneous differential equation.
Tap to see back →
Because the inhomogeneity does not take a form we can exploit with undetermined coefficients, we must use variation of parameters. Thus, first we find the complementary solution. The characteristic equation of  is
is  , with solutions of
, with solutions of  . This means that
. This means that  and
and  .
.
To do variation of parameters, we will need the Wronskian, 
Variation of parameters tells us that the coefficient in front of  is
is  where
where  is the Wronskian with the
is the Wronskian with the  row replaced with all 0's and a 1 at the bottom. In the 2x2 case this means that
row replaced with all 0's and a 1 at the bottom. In the 2x2 case this means that
 . Plugging in, the first half simplifies to
. Plugging in, the first half simplifies to

and the second half becomes 
Putting these together with the complementary solution, we have a general solution of 
Because the inhomogeneity does not take a form we can exploit with undetermined coefficients, we must use variation of parameters. Thus, first we find the complementary solution. The characteristic equation of 




To do variation of parameters, we will need the Wronskian,
Variation of parameters tells us that the coefficient in front of 




and the second half becomes
Putting these together with the complementary solution, we have a general solution of
Find a general solution to the following ODE

Find a general solution to the following ODE
Tap to see back →
We know the solution consists of a homogeneous solution and a particular solution.

The auxiliary equation for the homogeneous solution is

The homogeneous solution is

The particular solution is of the form

It requires variation of parameters to solve


Solving the system gets us


Integrating gets us


So 
Our solution is

We know the solution consists of a homogeneous solution and a particular solution.
The auxiliary equation for the homogeneous solution is
The homogeneous solution is
The particular solution is of the form
It requires variation of parameters to solve
Solving the system gets us
Integrating gets us
So
Our solution is