Exponential and Logarithmic Functions - College Algebra
Card 0 of 328
On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws  annual interest compounded continuously. The plan is for the value of the CD to be at least
annual interest compounded continuously. The plan is for the value of the CD to be at least  on the child's
on the child's  birthday.
birthday.
If the amount of money invested is to be a multiple of  , what is the minimum that should be invested initially, assuming that there are no further deposits or withdrawals?
, what is the minimum that should be invested initially, assuming that there are no further deposits or withdrawals?
On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws 


If the amount of money invested is to be a multiple of 
If we let  be the initial amount invested and
be the initial amount invested and  be the annual interest rate of the CD expressed as a decimal, then at the end of
be the annual interest rate of the CD expressed as a decimal, then at the end of  years, the amount of money
years, the amount of money 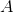 that the CD will be worth can be determined by the formula
that the CD will be worth can be determined by the formula

Substitute  ,
,  ,
, 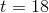 , and solve for
, and solve for  .
.

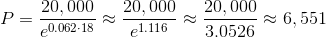
The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.
If we let 


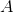
Substitute 

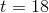

The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.
Compare your answer with the correct one above
Twelve years ago, your grandma put money into a savings account for you that earns  interest annually and is continuously compounded. How much money is currently in your account if she initially deposited
interest annually and is continuously compounded. How much money is currently in your account if she initially deposited  and you have not taken any money out?
and you have not taken any money out?
Twelve years ago, your grandma put money into a savings account for you that earns 

1. Use  where
where  is the current amount,
is the current amount,  is the interest rate,
is the interest rate,  is the amount of time in years since the initial deposit, and
is the amount of time in years since the initial deposit, and  is the amount initially deposited.
is the amount initially deposited.



2. Solve for 



You currently have $24,596 in your account.
1. Use 




2. Solve for
You currently have $24,596 in your account.
Compare your answer with the correct one above
Jeffrey has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Jeffrey deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded continuously. At the very beginning of each month, he deposits another $10,000. How much will he have at the very end of the year?
Jeffrey has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Jeffrey deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded continuously. At the very beginning of each month, he deposits another $10,000. How much will he have at the very end of the year?
The continuous compound interest formula is
 ,
,
where  is the amount of money in the account at the end of the period,
is the amount of money in the account at the end of the period,  is the principal at the beginning,
is the principal at the beginning,  is the annual interest rate in decimal form, and
is the annual interest rate in decimal form, and  is the number of years over which the interest accumulates. Since Jeff deposits $1,000 per month, we apply this formula twelve times, with
is the number of years over which the interest accumulates. Since Jeff deposits $1,000 per month, we apply this formula twelve times, with  equal to the principal at the beginning of each successive month,
equal to the principal at the beginning of each successive month,  , and
, and  .
.
We can go ahead and calculate  , since
, since  and
and  do not change:
do not change:

The formula can be rewritten as

At the beginning of January, Jeffrey deposits $10,000. At the end of January, there is

in the account.
At the beginning of February, he again deposits $10,000, so there is now

in the account.
At the end of February, there is

in the account.
Repeat addition of $10,000, then multiplication by 1.006353, ten more times to get the amount of money in the account at the end of December. This will be $125,072.98.
The continuous compound interest formula is

where 






We can go ahead and calculate 


The formula can be rewritten as
At the beginning of January, Jeffrey deposits $10,000. At the end of January, there is
in the account.
At the beginning of February, he again deposits $10,000, so there is now
in the account.
At the end of February, there is
in the account.
Repeat addition of $10,000, then multiplication by 1.006353, ten more times to get the amount of money in the account at the end of December. This will be $125,072.98.
Compare your answer with the correct one above
Sheila has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Sheila deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded monthly. At the very beginning of each month, she deposits another $10,000. How much will she have at the very end of the year?
Sheila has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Sheila deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded monthly. At the very beginning of each month, she deposits another $10,000. How much will she have at the very end of the year?
The periodic compound interest formula is

where  is the amount of money in the account at the end of the period,
is the amount of money in the account at the end of the period,  is the principal at the beginning,
is the principal at the beginning,  is the annual interest rate in decimal form,
is the annual interest rate in decimal form,  is the number of periods per year at which the interest is compounded, and
is the number of periods per year at which the interest is compounded, and  is the number of years over which the interest accumulates.
is the number of years over which the interest accumulates.
Since Sheila deposits $1,000 per month, we apply this formula twelve times, with  equal to the principal at the beginning of each successive month,
equal to the principal at the beginning of each successive month,  ,
,  (monthly interest), and
(monthly interest), and  .
.
We can go ahead and calculate  , since
, since  ,
,  , and
, and  remain constant:
remain constant:
 .
.
The formula can be rewritten as

At the beginning of January, Sheila deposits $10,000. At the end of January, there is

in the account.
At the beginning of February, she again deposits $10,000, so there is now

in the account.
At the end of February, there is

in the account.
Repeat addition of $10,000, then multiplication by 1.006333, ten more times to get the amount of money in the account at the end of December. This will be $125.056.56
The periodic compound interest formula is
where 




Since Sheila deposits $1,000 per month, we apply this formula twelve times, with 



We can go ahead and calculate 




The formula can be rewritten as
At the beginning of January, Sheila deposits $10,000. At the end of January, there is
in the account.
At the beginning of February, she again deposits $10,000, so there is now
in the account.
At the end of February, there is
in the account.
Repeat addition of $10,000, then multiplication by 1.006333, ten more times to get the amount of money in the account at the end of December. This will be $125.056.56
Compare your answer with the correct one above
Solve for y in the following expression:

Solve for y in the following expression:
To solve for y we first need to get rid of the logs.

Then we get  .
.
After that, we simply have to divide by 5x on both sides:

To solve for y we first need to get rid of the logs.
Then we get 
After that, we simply have to divide by 5x on both sides:
Compare your answer with the correct one above
An investor places $5,000 into an account that has a 5% interest rate. If the he keeps his money in the account for 57 months, and it is compounded quarterly, how much interest will he earn?
Round your answer to the nearest dollar, if needed
An investor places $5,000 into an account that has a 5% interest rate. If the he keeps his money in the account for 57 months, and it is compounded quarterly, how much interest will he earn?
Round your answer to the nearest dollar, if needed
Use the formula for compound interest to solve: 
"A" is the amount of interest, "P" is the initial amount invested, "r" is the interest rate, "m" is the number of times per year the interest is compounded, and "t" is the number of years the money is invested.
Plug in the appropriate values for the equation: 
Because "t" is measure in years, 57 months needs to be converted to years (i.e. 57 months=4.75 years) to solve this equation
Simplify the equation: 
Solution: 
Use the formula for compound interest to solve:
"A" is the amount of interest, "P" is the initial amount invested, "r" is the interest rate, "m" is the number of times per year the interest is compounded, and "t" is the number of years the money is invested.
Plug in the appropriate values for the equation:
Because "t" is measure in years, 57 months needs to be converted to years (i.e. 57 months=4.75 years) to solve this equation
Simplify the equation:
Solution:
Compare your answer with the correct one above
Which equation is equivalent to:

Which equation is equivalent to:
 ,
, 

So, 

So,
Compare your answer with the correct one above

What is the inverse of the log function?
What is the inverse of the log function?
This is a general formula that you should memorize. The inverse of  is
is  . You can use this formula to change an equation from a log function to an exponential function.
. You can use this formula to change an equation from a log function to an exponential function.
This is a general formula that you should memorize. The inverse of 

Compare your answer with the correct one above
Solve: 
Solve:
To solve  , it is necessary to know the property of
, it is necessary to know the property of  .
.

Since  and the
and the  terms cancel due to inverse operations, the answer is what's left of the
terms cancel due to inverse operations, the answer is what's left of the  term.
term.
The answer is: 
To solve 

Since 


The answer is:
Compare your answer with the correct one above
Rewrite the following expression as an exponential expression:

Rewrite the following expression as an exponential expression:
Rewrite the following expression as an exponential expression:

Recall the following property of logs and exponents:

Can be rewritten in the following form:

So, taking the log we are given;

We can rewrite it in the form:

So b must be a really huge number!
Rewrite the following expression as an exponential expression:
Recall the following property of logs and exponents:
Can be rewritten in the following form:
So, taking the log we are given;
We can rewrite it in the form:
So b must be a really huge number!
Compare your answer with the correct one above
Convert the following logarithmic equation to an exponential equation:

Convert the following logarithmic equation to an exponential equation:
Convert the following logarithmic equation to an exponential equation:

Recall the following:
This

Can be rewritten as

So, our given logarithm

Can be rewritten as

Fortunately we don't need to expand, because this woud be a very large number!
Convert the following logarithmic equation to an exponential equation:
Recall the following:
This
Can be rewritten as
So, our given logarithm
Can be rewritten as
Fortunately we don't need to expand, because this woud be a very large number!
Compare your answer with the correct one above
Convert the following logarithmic equation to an exponential equation.

Convert the following logarithmic equation to an exponential equation.
Convert the following logarithmic equation to an exponential equation.

To convert from logarithms to exponents, recall the following property:

Can be rewritten as:

So, starting with
 ,
,
We can get

Convert the following logarithmic equation to an exponential equation.
To convert from logarithms to exponents, recall the following property:
Can be rewritten as:
So, starting with

We can get
Compare your answer with the correct one above
Solve the following:

Solve the following:
To solve the following, you must "undo" the 5 with taking log based 5 of both sides. Thus,



The right hand side can be simplified further, as 125 is a power of 5. Thus,



To solve the following, you must "undo" the 5 with taking log based 5 of both sides. Thus,
The right hand side can be simplified further, as 125 is a power of 5. Thus,
Compare your answer with the correct one above
Solve for  :
:

(Nearest hundredth)
Solve for 
(Nearest hundredth)
Apply the Product of Powers Property to rewrite the second expression:



Distribute out:


Divide both sides by 5:


Take the natural logarithm of both sides (and note that you can use common logarithms as well):

Apply a property of logarithms:

Divide by  and evaluate:
and evaluate:



Apply the Product of Powers Property to rewrite the second expression:
Distribute out:
Divide both sides by 5:
Take the natural logarithm of both sides (and note that you can use common logarithms as well):
Apply a property of logarithms:
Divide by 
Compare your answer with the correct one above
Solve for  :
:

(Nearest hundredth, if applicable).
Solve for 
(Nearest hundredth, if applicable).
 , so rewrite the expression at right as a power of 3 using the Power of a Power Property:
, so rewrite the expression at right as a power of 3 using the Power of a Power Property:



Set the exponents equal to each other and solve the resulting linear equation:

Distribute:

Subtract  and 1 from both sides; we can do this simultaneously:
and 1 from both sides; we can do this simultaneously:


Divide by  :
:



Set the exponents equal to each other and solve the resulting linear equation:
Distribute:
Subtract 
Divide by 
Compare your answer with the correct one above
Solve the following for x:

Solve the following for x:
To solve, you must first "undo" the log. Since no base is specified, you assume it is 10. Thus, we need to take 10 to both sides.


Now, simply solve for x.


To solve, you must first "undo" the log. Since no base is specified, you assume it is 10. Thus, we need to take 10 to both sides.
Now, simply solve for x.
Compare your answer with the correct one above
Simplify the following:

Simplify the following:
To solve, you must combine the logs into 1 log, instead of three separate ones. To do this, you must remember that when adding logs, you multiply their insides, and when you subtract them, you add their insides. Therefore,



To solve, you must combine the logs into 1 log, instead of three separate ones. To do this, you must remember that when adding logs, you multiply their insides, and when you subtract them, you add their insides. Therefore,
Compare your answer with the correct one above
Find the value of a:

Find the value of a:
For this problem, we can use the fact that the exponent and logarithm are inverses of each other. So if we raise both sides up as exponents:

The left side of the equation cancels and we get that

For this problem, we can use the fact that the exponent and logarithm are inverses of each other. So if we raise both sides up as exponents:
The left side of the equation cancels and we get that
Compare your answer with the correct one above
Solve for  .
.

Solve for 
To solve this natural logarithm equation, we must eliminate the  operation. To do that, we must remember that
operation. To do that, we must remember that  is simply
is simply  with base
with base  . So, we raise both side of the equation to the
. So, we raise both side of the equation to the  power.
power.

This simplifies to
 . Remember that anything raised to the 0 power is 1.
. Remember that anything raised to the 0 power is 1.
Continuing to solve for x,


To solve this natural logarithm equation, we must eliminate the 




This simplifies to

Continuing to solve for x,
Compare your answer with the correct one above
Solve for  .
.

Solve for 
To eliminate the  operation, simply raise both side of the equation to the
operation, simply raise both side of the equation to the  power because the base of the
power because the base of the  operation is 7.
operation is 7.

This simplifies to



To eliminate the 


This simplifies to
Compare your answer with the correct one above