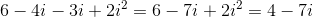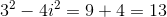Complex Numbers - College Algebra
Card 0 of 108
Add:
Add:
Tap to see back →
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives 
, and adding the imaginary parts gives 
.
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives
Divide: 
The answer must be in standard form.
Divide:
The answer must be in standard form.
Tap to see back →
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
which results in
The numerator after simplification give us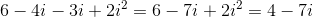 
The denominator is equal to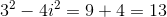 
Hence, the final answer in standard form =
Multiply both the numerator and the denominator by the conjugate of the denominator which is
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
Divide: 
Answer must be in standard form.
Divide:
Answer must be in standard form.
Tap to see back →
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
resulting in
This is equal to 
Since 
you can make that substitution of 
in place of 
in both numerator and denominator, leaving:
When you then cancel the negatives in both numerator and denominator (remember that 
, simplifying each term), you're left with a denominator of 
and a numerator of 
, which equals 
.
Multiply both the numerator and the denominator by the conjugate of the denominator which is
This is equal to
Since 
When you then cancel the negatives in both numerator and denominator (remember that 
Consider the following definitions of imaginary numbers:
Then, 
Consider the following definitions of imaginary numbers:
Then,
Tap to see back →
What is the value of 
?
What is the value of
Tap to see back →
Recall that the definition of imaginary numbers gives that 
and thus that 
. Therefore, we can use Exponent Rules to write 
Recall that the definition of imaginary numbers gives that
What is the value of 
?
What is the value of
Tap to see back →
When dealing with imaginary numbers, we multiply by foiling as we do with binomials. When we do this we get the expression below:
Since we know that 
we get 
which gives us 
.
When dealing with imaginary numbers, we multiply by foiling as we do with binomials. When we do this we get the expression below:
Since we know that
Evaluate: 
Evaluate:
Tap to see back →
Use the FOIL method to simplify. FOIL means to mulitply the first terms together, then multiply the outer terms together, then multiply the inner terms togethers, and lastly, mulitply the last terms together.
The imaginary 
is equal to:
Write the terms for 
.
Replace 
with the appropiate values and simplify.
Use the FOIL method to simplify. FOIL means to mulitply the first terms together, then multiply the outer terms together, then multiply the inner terms togethers, and lastly, mulitply the last terms together.
The imaginary
Write the terms for
Replace
Tap to see back →
Combine like terms:
Distribute:
Combine like terms:
Combine like terms:
Distribute:
Combine like terms:
Multiply: 
Multiply:
Tap to see back →
Use FOIL to multiply the two binomials.
Recall that FOIL stands for Firsts, Outers, Inners, and Lasts.
Remember that 
Use FOIL to multiply the two binomials.
Recall that FOIL stands for Firsts, Outers, Inners, and Lasts.
Remember that
Rationalize the complex fraction: 
Rationalize the complex fraction:
Tap to see back →
To rationalize a complex fraction, multiply numerator and denominator by the conjugate of the denominator.
To rationalize a complex fraction, multiply numerator and denominator by the conjugate of the denominator.
Simplify the following:
Simplify the following:
Tap to see back →
To solve, you must remember the basic rules for i exponents.
Given the prior, simply plug into the given expression and combine like terms.
To solve, you must remember the basic rules for i exponents.
Given the prior, simply plug into the given expression and combine like terms.
Given the following quadratic, which values of 
will produce a set of complex valued solutions for 
Given the following quadratic, which values of
Tap to see back →
In order to determine if a quadratic equation 
will have real-valued or complex-valued solutions compute the discriminate:
If the discriminate is negative, we will have complex-valued solutions. If the discriminate is positive, we will have real-valued solutions.
This arises from the fact that the quadratic equation has the square-root term,
Evaluate the discriminate for 
-79<0 so the quadratic has complex roots for 
.
Evaluate the discriminate for 
The discriminate is positive, therefor the quadratic has real roots for 
In order to determine if a quadratic equation
If the discriminate is negative, we will have complex-valued solutions. If the discriminate is positive, we will have real-valued solutions.
This arises from the fact that the quadratic equation has the square-root term,
Evaluate the discriminate for
-79<0 so the quadratic has complex roots for
Evaluate the discriminate for
The discriminate is positive, therefor the quadratic has real roots for
Evaluate: 
Evaluate:
Tap to see back →
Recall that 
, 
, and 
.
Each imaginary term can then be factored by using 
.
Replace the numerical values for each term.
The answer is: 
Recall that
Each imaginary term can then be factored by using
Replace the numerical values for each term.
The answer is:
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the negative:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 2+4i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the negative:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 2+4i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10-4i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10-4i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10+2i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10+2i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 7+18i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 7+18i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 9+2i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 9+2i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of -1+9i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of -1+9i
Simplify:
Simplify:
Tap to see back →
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10-4i
When simplifying expressions with complex numbers, use the same techniques and procedures as normal.
Distribute the sign to the terms in parentheses:
Combine like terms- combine the real numbers together and the imaginary numbers together:
This gives a final answer of 10-4i