Using Probability to Make Decisions - AP Statistics
Card 0 of 348
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 3, Coin 5
The coin that is the least fair is: Coin 3


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 3, Coin 5
The coin that is the least fair is: Coin 3
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 1


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 1
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
s= 0.02
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
s= 0.02
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 4


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 4
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5
Compare your answer with the correct one above
Lauren has a computer programming assignment to create a random number generator that generates numbers on the interval ![[0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/184859/gif.latex) .
.
Which of the following statements must be TRUE about the random number generator if it is fair?
Lauren has a computer programming assignment to create a random number generator that generates numbers on the interval ![[0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/184859/gif.latex)
Which of the following statements must be TRUE about the random number generator if it is fair?
No explanation available
No explanation available
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coin is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coin is least fair according to the standard deviation?

This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:


Only one coin possesses probabilities outside of this range: "coin 3." This coin posses the following probabilities:


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
Only one coin possesses probabilities outside of this range: "coin 3." This coin posses the following probabilities:
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coin is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coin is least fair according to the standard deviation?

This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:


Only one coin possesses probabilities outside of this range: "coin 3." This coin posses the following probabilities:


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
Only one coin possesses probabilities outside of this range: "coin 3." This coin posses the following probabilities:
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 4


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 4
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 2, Coin 4, Coin 5
The coin that is the least fair is: Coin 4


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 2, Coin 4, Coin 5
The coin that is the least fair is: Coin 4
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 4, Coin 5
The coin that is the least fair is: Coin 1


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 4, Coin 5
The coin that is the least fair is: Coin 1
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 5
The coin that is the least fair is: Coin 3


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 5
The coin that is the least fair is: Coin 3
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 4, Coin 5
The coin that is the least fair is: Coin 1


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 4, Coin 5
The coin that is the least fair is: Coin 1
Compare your answer with the correct one above
Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:

They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?

Referees at a professional football game need to choose a coin for the pre-game coin toss. Studies have shown that a fair coin possesses the following standard deviation:
They test five coins by flipping them one hundred times and noting how many times each lands on heads or tails. Which of the following coins is least fair according to the standard deviation?
This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:


We know the standard deviation equals the following:

This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:

The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5


This standard relates to our ability to use probability to make fair decisions. Other standards used the expected means formula in order to calculate expected payoffs of games, lottery drawings, insurance policies, business ventures, and others. This information was then used in order to help us make decisions on whether to play games, invest in a company, or choose an insurance policy. Likewise, the essence of this standard is related to fairness or using probabilities to make fair decisions. In order to answer this question we need to discuss probabilities and the concept of fairness in events. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how fairness is described in chance events. In this sense, fairness is associated with randomness. This means that there is no bias being imparted upon the decision in the event. In other words, there is no bias on the part of the individuals nor is there a bias on the part the device being used to produce the outcome of the event. This means that the decision produced from the chance event will be “fair.” It is important to note that deviations from expected probabilities may occur. For instance, a person may roll a six on a fair die six times in a row. According to probability, we would expect a die to land with the six-side facing upwards only once out of six rolls; however, the process of deviation can help explain this phenomenon.
Suppose we rolled a fair die ten times and recorded the distribution. Next, we decided to do this an infinite number of times. We would create a "bell" shaped curve. In this curve the center would represent events that are likely to occur, such as rolling each side of the die on average one out of six times. The tails or extremes of the curve represent unlikely events that may occur but are highly unlikely, such as rolling one side of the die six times in a row. The dead center of the curve represents the mean and the standard deviation measures how far—under standard conditions—we can expect a sample to deviate or vary from the mean. in other words, if a set of dice consistently roll the same value many times, then we can assume that they may have been rigged or altered.

Probability rests upon the concepts of fairness and randomness. These terms are not necessarily synonymous. Fairness relates to the devices being used (e.g. coin, deck of cards, or die). On the other hand, randomness is an essential component of any statistical measure and indicates that every outcome has an equal chance of occurring. Now, let's use this information to solve the problem.
In order to solve this problem, we need to calculate how the probability varies under standard conditions according to the standard deviation. We know that we have a one out of two chance of flipping a coin to heads or tails; therefore, we can write the following probabilities:
We know the standard deviation equals the following:
This means that the probability may vary by this amount; therefore, a fair coin may possess the following probabilities:
The following coins possess probabilities outside of this range:, Coin 1, Coin 2, Coin 3, Coin 4, Coin 5
The coin that is the least fair is: Coin 5
Compare your answer with the correct one above
The Witches' Duel is a game of chance. On each turn, there are four possible outcomes:
You earn 1 point with probability .2, and you lose 1 point with probability .3.
You earn 5 points with probability .35, and you lose 5 points with probability .15.
On average, how many points do you earn on each turn?
The Witches' Duel is a game of chance. On each turn, there are four possible outcomes:
You earn 1 point with probability .2, and you lose 1 point with probability .3.
You earn 5 points with probability .35, and you lose 5 points with probability .15.
On average, how many points do you earn on each turn?
No explanation available
No explanation available
Compare your answer with the correct one above
A state lottery is holding a million dollar raffle and each ticket has the following odds of being a winner:

Which of the following choices best represents the price where tickets would start costing too much to play and expect to make money over the long run?
A state lottery is holding a million dollar raffle and each ticket has the following odds of being a winner:
Which of the following choices best represents the price where tickets would start costing too much to play and expect to make money over the long run?
This substandard specifically relates to calculating the expected payoff of a game of chance (e.g. the expected winnings from a state lottery or a game at a fast-food restaurant). In this standard, you will be asked to calculate the expected value of a payoff of a game in order to determine whether or not it is worth playing. In this manner, students’ will learn how probabilities can inform their decisions to enhance winnings or avoid losses at games of chance. This standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
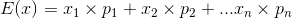
In this equation the variables are identified as the following:
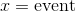

We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.

Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:




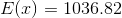
Round to the nearest one's place.
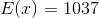
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We are told that the payoff for the raffle is one million dollars and we know that each ticket has the following chances of being a winner:

We will use the expected means formula and substitute the  variable for the given payoff for the lottery ticket. Substitute the given information into the formula.
variable for the given payoff for the lottery ticket. Substitute the given information into the formula.


Simplify.

Solve.

In the long run, the expected payoff is eight dollars. In other words, if we were to buy all the tickets we would break even at one million dollars if each only cost eight dollars. If the tickets cost more than this number, then it is not worth it to purchase a ticket when we associate this with the expected payoff. We need to choose the answer that is directly greater than eight dollars; therefore, the following choice is correct:

This substandard specifically relates to calculating the expected payoff of a game of chance (e.g. the expected winnings from a state lottery or a game at a fast-food restaurant). In this standard, you will be asked to calculate the expected value of a payoff of a game in order to determine whether or not it is worth playing. In this manner, students’ will learn how probabilities can inform their decisions to enhance winnings or avoid losses at games of chance. This standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We are told that the payoff for the raffle is one million dollars and we know that each ticket has the following chances of being a winner:
We will use the expected means formula and substitute the 
Simplify.
Solve.
In the long run, the expected payoff is eight dollars. In other words, if we were to buy all the tickets we would break even at one million dollars if each only cost eight dollars. If the tickets cost more than this number, then it is not worth it to purchase a ticket when we associate this with the expected payoff. We need to choose the answer that is directly greater than eight dollars; therefore, the following choice is correct:
Compare your answer with the correct one above
A winning raffle ticket has the following payout scheme:
\$1 with probability .25
\$10 with probability .35
\$100 with probability .29
\$1,000 with probability .1
\$10,000 with probability .01
What is the expected payout for a winning raffle ticket?
A winning raffle ticket has the following payout scheme:
\$1 with probability .25
\$10 with probability .35
\$100 with probability .29
\$1,000 with probability .1
\$10,000 with probability .01
What is the expected payout for a winning raffle ticket?
No explanation available
No explanation available
Compare your answer with the correct one above
At Moe's Pizzeria customers can get a free slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting three or fewer free slices of pizza in eleven visits to Moe's?
At Moe's Pizzeria customers can get a free slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting three or fewer free slices of pizza in eleven visits to Moe's?
In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
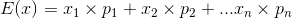
In this equation the variables are identified as the following:
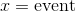

We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.

Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:




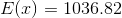
Round to the nearest one's place.
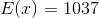
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:

Remember that in combinations and permutations a combination is calculated using the following formula:

Now, we can write the following formula.

In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable  . The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.
. The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:

In our formula the variables will equal the following:




Let's solve for each of the four probabilities starting with the probability of not getting a slice in the eleven visits.

Remember that the factorial of zero equals one and that any number raised to a power of zero equals one.



Next, we will solve for the probability of getting a single slice.



Next, we will solve for the probability of getting two slices.



Last, we will solve for the probability of getting three slices.



Now, we need to add these together to get the answer. We need to add them because we need to find the probabilities of getting three or fewer slices in eleven visits.


Round to three decimal places.

In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:
Remember that in combinations and permutations a combination is calculated using the following formula:
Now, we can write the following formula.
In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable 

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:
In our formula the variables will equal the following:
Let's solve for each of the four probabilities starting with the probability of not getting a slice in the eleven visits.
Remember that the factorial of zero equals one and that any number raised to a power of zero equals one.
Next, we will solve for the probability of getting a single slice.
Next, we will solve for the probability of getting two slices.
Last, we will solve for the probability of getting three slices.
Now, we need to add these together to get the answer. We need to add them because we need to find the probabilities of getting three or fewer slices in eleven visits.
Round to three decimal places.
Compare your answer with the correct one above
At a Moe's Pizzeria customers can get a fee slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting three or fewer free slices of pizza in eleven visits to Moe's?
At a Moe's Pizzeria customers can get a fee slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting three or fewer free slices of pizza in eleven visits to Moe's?
In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
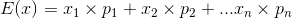
In this equation the variables are identified as the following:
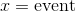

We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:




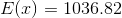
Round to the nearest one's place.
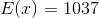
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:

Remember that in combinations and permutations a combination is calculated using the following formula:

Now, we can write the following formula.

In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable  . The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.
. The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:

In our formula the variables will equal the following:




Let's solve for each of the four probabilities starting with the probability of not getting a slice in the eleven visits.

Remember that the factorial of zero equals one and that any number raised to a power of zero equals one.



Next, we will solve for the probability of getting a single slice.



Next, we will solve for the probability of getting two slices.



Last, we will solve for the probability of getting three slices.



Now, we need to add these together to get the answer. We need to add them because we need to find the probabilities of getting three or fewer slices in eleven visits.


Round to three decimal places.

In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:
Remember that in combinations and permutations a combination is calculated using the following formula:
Now, we can write the following formula.
In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable 

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:
In our formula the variables will equal the following:
Let's solve for each of the four probabilities starting with the probability of not getting a slice in the eleven visits.
Remember that the factorial of zero equals one and that any number raised to a power of zero equals one.
Next, we will solve for the probability of getting a single slice.
Next, we will solve for the probability of getting two slices.
Last, we will solve for the probability of getting three slices.
Now, we need to add these together to get the answer. We need to add them because we need to find the probabilities of getting three or fewer slices in eleven visits.
Round to three decimal places.
Compare your answer with the correct one above
At Moe's Pizzeria customers can get a free slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting zero free slices of pizza in eleven visits to Moe's?
At Moe's Pizzeria customers can get a free slice by landing a quarter in a glass nestled in a large jug of water. A customer has a one in eleven chance of getting a quarter into the glass. What are the chances of getting zero free slices of pizza in eleven visits to Moe's?
In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:


Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.

According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
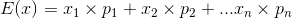
In this equation the variables are identified as the following:
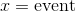

We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.

Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:




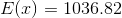
Round to the nearest one's place.
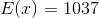
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:

Remember that in combinations and permutations a combination is calculated using the following formula:

Now, we can write the following formula.

In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable  . The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.
. The researcher can roll an even number every time he rolls and he may not even roll an even number in all twelve trial. We need to calculate this probability for every possible number of successful events; therefore, the number of successes ranges from zero to twelve. Last, we know that there are a total of twelve trials. We have solved for the probability of each of these variables for every possible number of successes in the trials.

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:

In our formula the variables will equal the following:

Let's solve for the probability.


This in scientific notation is

In order to solve this problem, we need to discuss probabilities and their applications in the calculation of expected means and the creation of probability distribution models and. Problems associated with this standard will require you to calculate expected values and distinguish random variables. This means that you must understand when an event has equal or differing probabilities. Afterwards, you must determine what the problem is asking you to calculate (i.e. probability, expected value, or actual average) and apply the lessons learned in the expected means and probability distribution model lessons. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle engine sizes with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Finally, we need to determine how we will discuss how to create a probability distribution graph for a probability model. We will use the following equation to calculate the probabilities to be used in this graphical display:
Remember that in combinations and permutations a combination is calculated using the following formula:
Now, we can write the following formula.
In this formula variables are defined in the following manner:

Let's investigate this standard through the use of an example. Suppose a researcher rolls a die twelve times and notes whether the die rolls on an even or an odd number. If the die is fair (i.e. every number has an equal probability of being rolled or each roll is random), then would the probability distribution graph follow the pattern of a normal distribution? Lets create a table and solve for each variable. The probability of rolling an even number—a two, four, or a six— is three out of six or fifty percent. Likewise, the probability of failure (i.e. rolling an odd number) is three out of six or fifty percent. Next, we need to list the number of successes for each event—variable 

Once this data is tabulated we can graph the probability of rolling an even number. If we look at the graph then we can see if it follows the bell shape curve of a normal distribution.

A bell curve is shaped like the following image:

We can quickly tell that the graph of the probability distribution does follow the shape of a normal or "bell" curve.
Now, we can use this information to solve the given problem. In order to solve this problem we need to create a probability distribution model for the chances of getting zero to three slices in the eleven visits. The probability of getting three or fewer slices will be the sum of these four probabilities. We need to use the following formula:
In our formula the variables will equal the following:
Let's solve for the probability.
This in scientific notation is
Compare your answer with the correct one above




































































