Random Variables - AP Statistics
Card 0 of 88
Which of the following is NOT a discrete random variable?
Which of the following is NOT a discrete random variable?
Tap to see back →
By definition, a discrete random variable is a random variable whose values can be "counted" one by one. A continuous random variable is a random variable that can take any value on a certain interval. Of these choices, the number of lip products, the amount of money, and the number of midterms taken are all discrete random variables, as the respective values can be counted; however, the time taken to watch the first four seasons of a TV show is a continuous random variable, as not everyone will take the same amount of time to watch all those episodes (i.e. some might fastf-orward/replay parts of episodes).
By definition, a discrete random variable is a random variable whose values can be "counted" one by one. A continuous random variable is a random variable that can take any value on a certain interval. Of these choices, the number of lip products, the amount of money, and the number of midterms taken are all discrete random variables, as the respective values can be counted; however, the time taken to watch the first four seasons of a TV show is a continuous random variable, as not everyone will take the same amount of time to watch all those episodes (i.e. some might fastf-orward/replay parts of episodes).
We have two independent, normally distributed random variables  and
and  such that
such that  has mean
has mean  and variance
and variance  and
and  has mean
has mean  and variance
and variance  . What is the probability distribution of the difference of the random variables,
. What is the probability distribution of the difference of the random variables,  ?
?
We have two independent, normally distributed random variables 








Tap to see back →
The mean for any set of random variables is additive in the sense that

The difference is also additive, so we have

This means the mean of  is
is  .
.
The variance is additive when the random variables are independent, which they are in this case. But it's additive in the sense that for any real numbers  (even when negative), we have
(even when negative), we have
 .
.
So for this difference, we have

 .
.
So the mean and variance are  and
and  , respectively. In addition to that,
, respectively. In addition to that,  is normally distributed because the sum or difference of any set of independent normal random variables is also normally distributed.
is normally distributed because the sum or difference of any set of independent normal random variables is also normally distributed.
The mean for any set of random variables is additive in the sense that
The difference is also additive, so we have
This means the mean of 

The variance is additive when the random variables are independent, which they are in this case. But it's additive in the sense that for any real numbers 

So for this difference, we have

So the mean and variance are 


Variable  has a Poisson distribution with a mean of
has a Poisson distribution with a mean of 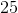 . What is the variance of Variable
. What is the variance of Variable  ?
?
Variable 
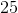

Tap to see back →
Because  has a Poisson distribution we know that:
has a Poisson distribution we know that:
 and
and
 .
.
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
Because 


Therefore, since we are given the mean of 25, we can find its variance to also be 25.
Tap to see back →
No explanation available
No explanation available
Tap to see back →
No explanation available
No explanation available
Let us suppose you are a waiter. You work your first four shifts and receive the following in tips: (1) 20, (2) 30, (3) 15, (4) 5. What is the mean amount of tips you will receive in a given day?
Let us suppose you are a waiter. You work your first four shifts and receive the following in tips: (1) 20, (2) 30, (3) 15, (4) 5. What is the mean amount of tips you will receive in a given day?
Tap to see back →
The answer is 17.5. Simply take the values for each day, add them, and divide by the total number of days to obtain the mean: 
The answer is 17.5. Simply take the values for each day, add them, and divide by the total number of days to obtain the mean:
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the mean outcome for the number of hours that Robert will work?
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the mean outcome for the number of hours that Robert will work?
Tap to see back →
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean. First, multiply each possible outcome by the probability of that outcome occurring. Second, add these results together.

We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean. First, multiply each possible outcome by the probability of that outcome occurring. Second, add these results together.
There are  collectable coins in a bag.
collectable coins in a bag.  are
are  ounces,
ounces,  are
are  ounces,
ounces,  are
are  ounces, and
ounces, and  are
are  ounces. If one coin is randomly selected, what is the mean possible weight in ounces?
ounces. If one coin is randomly selected, what is the mean possible weight in ounces?
There are 








Tap to see back →
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean.
First, multiply each possible outcome by the probability of that outcome occurring.
Second, add these results together.

We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean.
First, multiply each possible outcome by the probability of that outcome occurring.
Second, add these results together.
A basketball player makes  of his three-point shots. If he takes
of his three-point shots. If he takes  three-point shots each game, how many points per game does he score from three-point range?
three-point shots each game, how many points per game does he score from three-point range?
A basketball player makes 

Tap to see back →
First convert  .
.
The player's three-point shooting follows a binomial distribution with  and
and  .
.
On average, he thus makes  three-point shots per game.
three-point shots per game.
This means he averages 12 points per game from three-point range if he tries to make 10 three-pointers per game.

First convert 
The player's three-point shooting follows a binomial distribution with 

On average, he thus makes 
This means he averages 12 points per game from three-point range if he tries to make 10 three-pointers per game.
Tim samples the average plant height of potato plants for his science class and finds the following distribution (in inches):

Which of the following is/are true about the data?
i: the mode is 
ii: the mean is 
iii: the median is 
iv: the range is 
Tim samples the average plant height of potato plants for his science class and finds the following distribution (in inches):
Which of the following is/are true about the data?
i: the mode is
ii: the mean is
iii: the median is
iv: the range is
Tap to see back →
Analyzing the data, there are more 6s than anything else (mode), the median is between  and
and 
 , the mean is
, the mean is  , and the range is
, and the range is 
Analyzing the data, there are more 6s than anything else (mode), the median is between 



During a week's worth of soccer practice, a player practices  total free kicks and has a
total free kicks and has a  chance of scoring. What is the probability that he or she scored at least
chance of scoring. What is the probability that he or she scored at least  times? Assume each shot is independent.
times? Assume each shot is independent.
During a week's worth of soccer practice, a player practices 


Tap to see back →
Two steps are crucial here.
First, we need to recognize this is a binomial distribution with  and
and  .
.
Second, we need to realize we can use a normal approximation of the binomial since  and
and  , which are both larger than 5.
, which are both larger than 5.
With that said, we can calculate a  -score and its
-score and its  -value, keeping in mind that our mean will be
-value, keeping in mind that our mean will be  and our standard deviation will be
and our standard deviation will be  , which is about
, which is about  .
.


Two steps are crucial here.
First, we need to recognize this is a binomial distribution with 

Second, we need to realize we can use a normal approximation of the binomial since 

With that said, we can calculate a 




Which of the following would be considered a binomial experiment?
Which of the following would be considered a binomial experiment?
Tap to see back →
There are four conditions that need to be satisfied for a binomial experiment:
-
Each trial must have two outcomes.
-
Each trial must be independent.
-
All trials must be identical.
-
The probabilities of the outcomes remain constant must not change with each trial.
The only choice that satisfies all four of these conditions (and is therefore a binomial experiment) is the rock-paper-scissors scenario.
There are four conditions that need to be satisfied for a binomial experiment:
-
Each trial must have two outcomes.
-
Each trial must be independent.
-
All trials must be identical.
-
The probabilities of the outcomes remain constant must not change with each trial.
The only choice that satisfies all four of these conditions (and is therefore a binomial experiment) is the rock-paper-scissors scenario.
Suppose you are throwing three darts and you have a one third chance of hitting the bull's eye. Each throw is independent of one another. What is the chance of hitting the bull's eye at least once?
Suppose you are throwing three darts and you have a one third chance of hitting the bull's eye. Each throw is independent of one another. What is the chance of hitting the bull's eye at least once?
Tap to see back →
To calculate Prob(at least one bull's eye), we can instead compute one minus the complementary probability, P(no bull's eye).
So we have P(at least one bull's eye)=1-P(no bull's eye).
The chance of getting no bull's eyes is  .
.
This means the probability of getting at least one bull's eye is

To calculate Prob(at least one bull's eye), we can instead compute one minus the complementary probability, P(no bull's eye).
So we have P(at least one bull's eye)=1-P(no bull's eye).
The chance of getting no bull's eyes is 
This means the probability of getting at least one bull's eye is
A particle travels left with probability one sixth and right with probability five sixths. Each movement is independent of the others. What is the chance that after three movements, the particle ends up one unit to the right?
A particle travels left with probability one sixth and right with probability five sixths. Each movement is independent of the others. What is the chance that after three movements, the particle ends up one unit to the right?
Tap to see back →
The movements that this particle can make include: RRL, RLR, LRR.
The chance of getting RRL is  . This is also the chance of getting any of those movements.
. This is also the chance of getting any of those movements.
To get the total probability, we can add up the individual probabilities since the events are all mutually exclusive.
Thus, we get the following as the solution.

The movements that this particle can make include: RRL, RLR, LRR.
The chance of getting RRL is 
To get the total probability, we can add up the individual probabilities since the events are all mutually exclusive.
Thus, we get the following as the solution.
If you flip a biased coin, which has a  chance of being heads and
chance of being heads and  of being tails, until you get a head, what is the chance that it takes five flips until you get a head?
of being tails, until you get a head, what is the chance that it takes five flips until you get a head?
If you flip a biased coin, which has a 

Tap to see back →
To calculate this probability, we need to calculate the chance of getting 4 tails and then a head.
Each tail has a prob. of  and a head is
and a head is  , so we multiply
, so we multiply  to the power of 4 (because we need 4 tails) by
to the power of 4 (because we need 4 tails) by  (for the single head).
(for the single head).
So the probability is
 .
.
To calculate this probability, we need to calculate the chance of getting 4 tails and then a head.
Each tail has a prob. of 



So the probability is

Which of the following is a discrete random variable?
Which of the following is a discrete random variable?
Tap to see back →
A discrete variable is a variable which can only take a countable number of values. For example, the number of times that a coin can come up heads in ten flips can only be 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10. Thus, there are a countable number of possible outcomes (in this case 11). This is true for coin flips, but not for caterpillar length, water flow, or rates of return for stocks.
A discrete variable is a variable which can only take a countable number of values. For example, the number of times that a coin can come up heads in ten flips can only be 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10. Thus, there are a countable number of possible outcomes (in this case 11). This is true for coin flips, but not for caterpillar length, water flow, or rates of return for stocks.
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the standard deviation of the possible outcomes?
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the standard deviation of the possible outcomes?
Tap to see back →
There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Second, for each value in the group (45, 40, 25, and 12), subtract the mean from each and multiply the result by the probability of that outcome occurring. Third, add the four results together. Fourth, find the square root of the result.






There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Second, for each value in the group (45, 40, 25, and 12), subtract the mean from each and multiply the result by the probability of that outcome occurring. Third, add the four results together. Fourth, find the square root of the result.
If  and
and  are two independent random variables with
are two independent random variables with  and
and  , what is the standard deviation of the sum,
, what is the standard deviation of the sum, 
If 



Tap to see back →
If the random variables are independent, the variances are additive in the sense that
 .
.
So then the variance of the sum is
 .
.
The standard deviation is the square root of the variance, so we have
 .
.
If the random variables are independent, the variances are additive in the sense that

So then the variance of the sum is

The standard deviation is the square root of the variance, so we have

Consider the discrete random variable  that takes the following values with the corresponding probabilities:
that takes the following values with the corresponding probabilities:
 with
with 
 with
with 
 with
with 
Compute the probability  .
.
Consider the discrete random variable 
with
with
with
Compute the probability 
Tap to see back →
This probability is simple to compute:
We want to add the probability that X is greater or equal to two. This means the probability that X=2 or X=3.

Adding the necessary probabilities we arrive at the solution.


This probability is simple to compute:
We want to add the probability that X is greater or equal to two. This means the probability that X=2 or X=3.
Adding the necessary probabilities we arrive at the solution.
Consider the discrete random variable  that takes the following values with the corresponding probabilities:
that takes the following values with the corresponding probabilities:
 with
with 
 with
with 
 with
with 
 with
with 
Compute the expected value of the distribution.
Consider the discrete random variable 
with
with
with
with
Compute the expected value of the distribution.
Tap to see back →
The expected value is computed as
![\small \mathbb{E}[X]=\small $\sum_{x}$ xP(X=x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/348853/gif.latex)
for any values of x that the random variable takes.
So we have
![\small \small \mathbb{E}[X]= $\frac{1}{4}$\cdot 1+\frac{1}{4}$\cdot 2+\frac{1}{4}$\cdot 3+\frac{1}{4}$\cdot 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/348854/gif.latex)

The expected value is computed as
for any values of x that the random variable takes.
So we have