Confidence and Proportion - AP Statistics
Card 0 of 12
Tap to see back →
No explanation available
No explanation available
In a simple random sample of 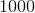 people,
people,  are left-handed. Find a
are left-handed. Find a  confidence interval for the true proportion of left-handed people in the entire population.
confidence interval for the true proportion of left-handed people in the entire population.
In a simple random sample of 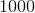


Tap to see back →
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is

Step 2:  , or the sample proportion is equal to
, or the sample proportion is equal to 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within  .
.

Step 4: Substitue all the values into the equation to get the answer.

Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
Tap to see back →
Tap to see back →
No explanation available
No explanation available
In a simple random sample of 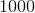 people,
people,  are left-handed. Find a
are left-handed. Find a  confidence interval for the true proportion of left-handed people in the entire population.
confidence interval for the true proportion of left-handed people in the entire population.
In a simple random sample of 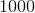


Tap to see back →
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is

Step 2:  , or the sample proportion is equal to
, or the sample proportion is equal to 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within  .
.

Step 4: Substitue all the values into the equation to get the answer.

Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
Tap to see back →
Tap to see back →
No explanation available
No explanation available
In a simple random sample of 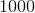 people,
people,  are left-handed. Find a
are left-handed. Find a  confidence interval for the true proportion of left-handed people in the entire population.
confidence interval for the true proportion of left-handed people in the entire population.
In a simple random sample of 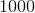


Tap to see back →
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is

Step 2:  , or the sample proportion is equal to
, or the sample proportion is equal to 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within  .
.

Step 4: Substitue all the values into the equation to get the answer.

Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
Tap to see back →
Tap to see back →
No explanation available
No explanation available
In a simple random sample of 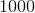 people,
people,  are left-handed. Find a
are left-handed. Find a  confidence interval for the true proportion of left-handed people in the entire population.
confidence interval for the true proportion of left-handed people in the entire population.
In a simple random sample of 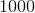


Tap to see back →
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is

Step 2:  , or the sample proportion is equal to
, or the sample proportion is equal to 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within  .
.

Step 4: Substitue all the values into the equation to get the answer.

Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
Tap to see back →

