Vector Form - AP Calculus BC
Card 0 of 70
Find the vector form of  to
to  .
.
Find the vector form of 

When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given  and
and 
![\overrightarrow{v}=[d-a, e-b, f-c]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327010/gif.latex)
In our case we have ending point at  and our starting point at
and our starting point at  .
.
Therefore we would set up the following and simplify.
![\overrightarrow{v}=[6-0,3-1,1-3]=[6,2,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327013/gif.latex)
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given 
In our case we have ending point at 

Therefore we would set up the following and simplify.
Compare your answer with the correct one above
In general:
If  ,
,
then 
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:

- Special rule when differentiating an exponential function:
 , where k is a constant.
, where k is a constant.
In this problem, 



Put it all together to get 

In general:
If 
then
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:
- Special rule when differentiating an exponential function:
, where k is a constant.
In this problem,
Put it all together to get
Compare your answer with the correct one above

Calculate 
Calculate
Calculate the sum of vectors.
In general,



Solution:




Calculate the sum of vectors.
In general,
Solution:
Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point
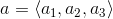 and
and  ,
,
the distance is the vector
 .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point
and
,
the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point 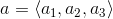 and
and  , the distance is the vector
, the distance is the vector  .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point and
, the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 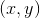 :
:


We can now use this value to solve for  :
:
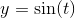

We can find the graph of 
:
We can now use this value to solve for :
Compare your answer with the correct one above
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 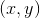 :
:




We can now use this value to solve for  :
:

We can find the graph of 
:
We can now use this value to solve for :
Compare your answer with the correct one above
Find the vector form of  to
to  .
.
Find the vector form of 

When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given  and
and 
![\overrightarrow{v}=[d-a, e-b, f-c]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327010/gif.latex)
In our case we have ending point at  and our starting point at
and our starting point at  .
.
Therefore we would set up the following and simplify.
![\overrightarrow{v}=[6-0,3-1,1-3]=[6,2,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327013/gif.latex)
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given 
In our case we have ending point at 

Therefore we would set up the following and simplify.
Compare your answer with the correct one above
In general:
If  ,
,
then 
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:

- Special rule when differentiating an exponential function:
 , where k is a constant.
, where k is a constant.
In this problem, 



Put it all together to get 

In general:
If 
then
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:
- Special rule when differentiating an exponential function:
, where k is a constant.
In this problem,
Put it all together to get
Compare your answer with the correct one above

Calculate 
Calculate
Calculate the sum of vectors.
In general,



Solution:




Calculate the sum of vectors.
In general,
Solution:
Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point
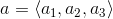 and
and  ,
,
the distance is the vector
 .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point
and
,
the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point 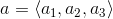 and
and  , the distance is the vector
, the distance is the vector  .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point and
, the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 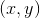 :
:


We can now use this value to solve for  :
:
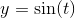

We can find the graph of 
:
We can now use this value to solve for :
Compare your answer with the correct one above
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 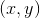 :
:




We can now use this value to solve for  :
:

We can find the graph of 
:
We can now use this value to solve for :
Compare your answer with the correct one above
Find the vector form of  to
to  .
.
Find the vector form of 

When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given  and
and 
![\overrightarrow{v}=[d-a, e-b, f-c]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327010/gif.latex)
In our case we have ending point at  and our starting point at
and our starting point at  .
.
Therefore we would set up the following and simplify.
![\overrightarrow{v}=[6-0,3-1,1-3]=[6,2,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327013/gif.latex)
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given 
In our case we have ending point at 

Therefore we would set up the following and simplify.
Compare your answer with the correct one above
In general:
If  ,
,
then 
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:

- Special rule when differentiating an exponential function:
 , where k is a constant.
, where k is a constant.
In this problem, 



Put it all together to get 

In general:
If 
then
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:
- Special rule when differentiating an exponential function:
, where k is a constant.
In this problem,
Put it all together to get
Compare your answer with the correct one above

Calculate 
Calculate
Calculate the sum of vectors.
In general,



Solution:




Calculate the sum of vectors.
In general,
Solution:
Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point
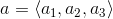 and
and  ,
,
the distance is the vector
 .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point
and
,
the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point 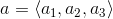 and
and  , the distance is the vector
, the distance is the vector  .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point and
, the distance is the vector
.
Subbing in our original points 

Compare your answer with the correct one above
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 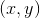 :
:


We can now use this value to solve for  :
:
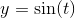

We can find the graph of 
:
We can now use this value to solve for :
Compare your answer with the correct one above
