Polar Form - AP Calculus BC

Card 0 of 210

Question

Rewrite in polar form:

Answer

$\left (r \cos \theta \right ) ^{2} = 3\left (r \cos \theta \right )\left (r \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta = 3 $r^{2}$ \cos \theta; \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta - 3 $r^{2}$ \cos \theta; \sin \theta \right ) = 1$

$r ^{2} \left ( \ \cos ^{2} \theta - 3 \cos \theta; \sin \theta \right ) = 1$

$r ^{2} = $\frac{1}{\cos ^{2}$ \theta - 3 \cos \theta; \sin \theta }$

$r =$\sqrt{ \frac{1}{\cos ^{2}$ \theta - 3 \cos \theta; \sin \theta }}$

Compare your answer with the correct one above

Question

Graph the equation $r=cos(\theta )$ where $0\leq \theta \leq2\pi$ .

Answer

At angle the graph as a radius of . As it approaches $\frac{\pi }{2}$ , the radius approaches .

As the graph approaches $\pi$ , the radius approaches .

Because this is a negative radius, the curve is drawn in the opposite quadrant between $\frac{3\pi }{2}$ and $2\pi$ .

Between $\pi$ and $\frac{3\pi }{2}$ , the radius approaches from and redraws the curve in the first quadrant.

Between $\frac{3\pi }{2}$ and $2\pi$ , the graph redraws the curve in the fourth quadrant as the radius approaches from .

Compare your answer with the correct one above

Question

Draw the graph of $r=cos(2\theta )$ from $0\leq \theta \leq2\pi$ .

Answer

Because this function has a period of $\pi$ , the x-intercepts of the graph happen at a reference angle of $\frac{\pi }{4}$ (angles halfway between the angles of the axes).

Between and $\frac{\pi }{4}$ the radius approaches from .

Between $\frac{\pi }{4}$ and $\frac{\pi }{2}$ , the radius approaches from and is drawn in the opposite quadrant, the third quadrant because it has a negative radius.

From $\frac{\pi }{2}$ to $\frac{3\pi }{4}$ the radius approaches from , and is drawn in the fourth quadrant, the opposite quadrant.

Between $\frac{3\pi }{4}$ and $\pi$ , the radius approaches from .

From $\pi$ and $\frac{5\pi }{4}$ , the radius approaches from .

Between $\frac{5\pi }{4}$ and $\frac{3\pi }{2}$ , the radius approaches from . Because it is a negative radius, it is drawn in the opposite quadrant, the first quadrant.

Then between $\frac{3\pi }{2}$ and $\frac{7\pi }{4}$ the radius approaches from and is draw in the second quadrant.

Finally between $\frac{7\pi }{4}$ and $2\pi$ , the radius approaches from .

Compare your answer with the correct one above

Question

What is the following coordinate in polar form?

Provide the angle in degrees.

Answer

To calculate the polar coordinate, use

$r=$\sqrt{29}$$

However, keep track of the angle here. 68 degree is the mathematical equivalent of the expression, but we know the point (-2,-5) is in the 3rd quadrant, so we have to add 180 to it to get 248.

Some calculators might already have provided you with the correct answer.

$\theta=248$ .

Compare your answer with the correct one above

Question

What is the equation in polar form?

Answer

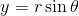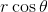We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given , then $r\sin \theta=2(r\cos \theta $)^{2}$$=2r^{2}$$\cos^{2}$ \theta$ .

$r\sin \theta=2(r\cos \theta $)^{2}$$=2r^{2}$$\cos^{2}$ \theta$ . Dividing both sides by $r\cos \theta$ ,

$\tan \theta=2r\cos \theta$

$$\frac{\tan \theta}{\cos \theta}$=2r$

$\tan \theta}{\sec \theta=2r$

$$\frac{1}{2}$\tan \theta}{\sec \theta=r$

Compare your answer with the correct one above

Question

What is the equation $y=\frac{6}{x}$$ in polar form?

Answer

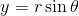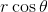We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given $y=\frac{6}{x}$$ , then $r\sin \theta=\frac{6}{r\cos \theta}$$ . Multiplying both sides by $r\cos \theta$ ,

$r=\sqrt$\frac{6}{\sin \theta cos \theta}$$

Compare your answer with the correct one above

Question

Convert the following function into polar form:

Answer

The following formulas were used to convert the function from polar to Cartestian coordinates:

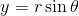$x=r\cos(\theta), y=r\sin(\theta), $x^2$$+y^2$$=r^2$$

Note that the last formula is a manipulation of a trignometric identity.

Simply replace these with x and y in the original function.

Compare your answer with the correct one above

Question

What is the equation in polar form?

Answer

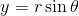We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=-$\frac{1}{2}$(r\cos $\theta)^{2}$$

Dividing both sides by $r\cos\theta$ , we get:

$\tan \theta=-$\frac{1}{2}$r\cos\theta$

$$\frac{\tan \theta}{\cos\theta}$=-$\frac{1}{2}$r$

$\tan \theta\sec\theta=-$\frac{1}{2}$r$

$r=-2\tan \theta\sec\theta$

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

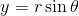We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

Dividing both sides by $r\cos\theta$ , we get:

$\tan\theta=-7r\cos\theta$

$$\frac{\tan\theta}{\cos\theta}$=-7r$

$\tan\theta\sec\theta=-7r$

$r=-$\frac{1}{7}$\tan\theta\sec\theta$

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

Dividing both sides by $r\cos\theta$ , we get:

$\tan\theta=-r\cos\theta$

$$\frac{\tan\theta}{\cos\theta}$=-r$

$\tan\theta\sec\theta=-r$

$r=-\tan\theta\sec\theta$

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=-10(r\cos\theta)+5$

$r\sin\theta+10(r\cos\theta)=5$

$r(\sin\theta+10\cos\theta)=5$

$r=\frac{5}{\sin\theta+10\cos\theta}$$

Compare your answer with the correct one above

Question

What is the polar form of $y=\frac{2}{3}$x+9$ ?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given $y=\frac{2}{3}$x+9$ , then:

$r\sin\theta= $\frac{2}{3}$(r\cos\theta)+9$

$r\sin\theta-$\frac{2}{3}$(r\cos\theta)=9$

$r(\sin\theta-$\frac{2}{3}$\cos\theta)=9$

$r=\frac{9}{\sin\theta-\frac{2}${3}\cos\theta}$

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=3-4(r\cos\theta)$

$r\sin\theta+4(r\cos\theta)=3$

$r(\sin\theta+4\cos\theta)=3$

$r=\frac{3}{\sin\theta+4\cos\theta}$$

Compare your answer with the correct one above

Question

Find the derivative of the following function:

$r=3\theta+e^\theta$

Answer

The derivative of a polar function is given by the following:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$\sin(\theta)+r\cos(\theta)}{$\frac{dr}{d\theta}$\cos(\theta)-r\sin(\theta)}$

First, we must find $$\frac{dr}{d\theta}$=3+e^\theta$

We found the derivative using the following rules:

$$\frac{\mathrm{d}$ }{\mathrm{d} $x}e^u$$=e^u$$\frac{\mathrm{du}$ }{\mathrm{d} x}$ , $\frac{\mathrm{d}$ }{\mathrm{d} $x}x^n$$=nx^{n-1}$

Finally, we plug in the above derivative and the original function into the above formula:

$\frac{(3+e^\theta)\sin(\theta)+(3\theta+e^\theta)\cos(\theta)}{(3+e^\theta)\cos(\theta)-(3\theta+e^\theta)\sin(\theta)}$

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

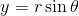We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=2(r\cos \theta)-7$

$r\sin\theta-2(r\cos \theta)=-7$

$r(\sin\theta-2\cos \theta)=-7$

$r=-$\frac{7}{\sin\theta-2\cos \theta}$$

Compare your answer with the correct one above

Question

What is the derivative of $r=4sin\theta+2$ ?

Answer

In order to find the derivative $\frac{dy}{dx}$ of a polar equation $r=4sin\theta+2$ , we must first find the derivative of with respect to $\theta$ as follows:

$$\frac{dr}{d\theta}$=4cos\theta$

We can then swap the given values of $\frac{dr}{d\theta}$ and into the equation of the derivative of an expression into polar form:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$sin\theta+rcos\theta}{$\frac{dr}{d\theta}$cos\theta-rsin\theta}$

$\frac{dy}{dx}$=\frac{4cos\theta\sin\theta+(4sin\theta+2)cos\theta}{4cos\theta\cos\theta-(4sin\theta+2)sin\theta}$

$\frac{dy}{dx}$=\frac{4cos\theta\sin\theta+4sin\theta\cos\theta+2\cos\theta}{4cos\theta\cos\theta-4sin\theta\sin\theta-2sin\theta}$

Using the trigonometric identity , we can deduce that . Swapping this into the denominator, we get:

Compare your answer with the correct one above

Question

What is the polar form of ?

Answer

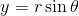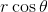We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=\frac{3}$9{}(r\cos $\theta)^{2}$$

Dividing both sides by $r\cos\theta$ , we get:

$\tan \theta=\frac{3}$9{}r\cos\theta$

$$\frac{\tan \theta}{\cos\theta}$=\frac{3}{9}$r$

$\tan \theta\sec\theta=\frac{3}{9}$r$

$r=\frac{9}{3}$\tan \theta\sec\theta$

$r=3\tan \theta\sec\theta$

Compare your answer with the correct one above

Question

Convert the following cartesian coordinates into polar form:

Answer

Cartesian coordinates have x and y, represented as (x,y). Polar coordinates have $(r,\theta)$

is the hypotenuse, and $\theta$ is the angle.

$r = $$\sqrt{x^2$$+y^2$}$$

$\theta = \arctan($\frac{y}{x}$)$

Solution:

$r = $$\sqrt{x^2$$+y^2$}$$

$r = $$\sqrt{(-3)^2$$+11^2$ }$= $\sqrt{(9+121)}$$

$r = $\sqrt{130}$$

$\theta = \arctan($\frac{y}{x}$)$

$\theta = \arctan(-$\frac{11}{3}$) = -74.74$

$($\sqrt{130}$,-74.74)$

Compare your answer with the correct one above

Question

Convert the following cartesian coordinates into polar form:

Answer

Cartesian coordinates have x and y, represented as (x,y). Polar coordinates have $(r,\theta)$

is the hypotenuse, and $\theta$ is the angle.

$r = $$\sqrt{x^2$$+y^2$}$$

$\theta = \arctan($\frac{y}{x}$)$

Solution:

$r = $$\sqrt{x^2$$+y^2$}$$

$r=$\sqrt{36+196}$$

$r=$\sqrt{232}$$

$\theta=\arctan($\frac{y}{x}$)$

$\theta=\arctan($\frac{-14}{6}$)$

$\theta=-66.8$

$($\sqrt{232}$,-66.8)$

Compare your answer with the correct one above

Question

What is the derivative of $r=2+5\sin\theta$ ?

Answer

In order to find the derivative $\frac{dy}{dx}$ of a polar equation $r=2+5\sin\theta$ , we must first find the derivative of with respect to $\theta$ as follows:

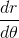$$\frac{dr}{d\theta}$=5\cos\theta$

We can then swap the given values of $\frac{dr}{d\theta}$ and into the equation of the derivative of an expression into polar form:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$\sin\theta+r\cos\theta}{$\frac{dr}{d\theta}$\cos\theta-r\sin\theta}$

$\frac{dy}{dx}$=\frac{(5\cos\theta)\sin\theta+(2+5\sin\theta)\cos\theta}{(5\cos\theta)\cos\theta-(2+5\sin\theta)\sin\theta}$

Using the trigonometric identity ![](https://lh3.googleusercontent.com/qHOZI-TYSmoUZca25iocJvaJo5lo7UOFpnRKgdd4_WnZLmZgdbZfX8GMlmTqeHc3sAuGGsKJG4zLkG9FEOQznFyOiJmHWuGk1bH-r50gZ1Gncp1EMUqk8hEF0-KplM6ZthvspP8 $"\sin^{2}$$\theta+\cos^{2}$\theta=1"), we can deduce that ![](https://lh6.googleusercontent.com/eok_ML9MG_sStGtoqEiLkZXNCirlZQ41YV4Jeclx1-Gy_BjdWZv2UfKut5ckGIphhajpaQnh4QN4Rs3SV47sUwK_3QN3O8SqSQuut3dIYiDamaNP5isQ_CBy_aLnDzOgnt8sLeQ $"\cos^{2}$$\theta=1-\sin^{2}$\theta"). Swapping this into the denominator, we get:

Compare your answer with the correct one above

Tap the card to reveal the answer