Parametric, Polar, and Vector Functions - AP Calculus BC

Card 0 of 984

Question

Rewrite as a Cartesian equation:

$x = t^{2} + 2t + 1, y = t^{2} - 2t + 1, t \in [-1, 1]$

Answer

$x = t^{2} + 2t + 1$

$x = \left ( t + 1\right )^{2}$

$\pm \sqrt{x} = t + 1$

So

$\sqrt{x} = t + 1$ or $-\sqrt{x} = t + 1$

We are restricting to values on $\left [ -1, 1\right ]$ , so is nonnegative; we choose

$\sqrt{x} = t + 1$ .

Also,

$y = t^{2} - 2t + 1$

$y= \left ( t - 1\right )^{2}$

$\sqrt{y} = \pm \left ( t - 1\right )$

So

$\sqrt{y} = t- 1$ or $-\sqrt{y} = t- 1$

We are restricting to values on $\left [ -1, 1\right ]$ , so is nonpositive; we choose

$-\sqrt{y} = t- 1$

or equivalently,

$\sqrt{y} = -t+ 1$

to make nonpositive.

Then,

$\sqrt{x}+ \sqrt{y} = (t + 1) + (-t + 1)$

and

$\sqrt{x}+ \sqrt{y} = 2$

$\sqrt{y} = 2 - \sqrt{x}$

$y =\left ( 2 - \sqrt{x} \right )^2$

$y = 4 - 4\sqrt{x} + \left (\sqrt{x} \right )^{2}$

$y = x + 4 - 4\sqrt{x}$

Compare your answer with the correct one above

Question

Rewrite as a Cartesian equation:

$x =10^ {t}, y = \sinh t, t \in (0,\infty )$

Answer

$y = \sinh t = \frac{e ^{2t} -1}{2e ^{t}} = \frac{\left (e ^{ t} \right) ^{2} -1}{2e ^{t}}$

$e^{t} = 10 ^{\log e \cdot t} =\left ( 10 ^{ t} \right )^{\log e} = x ^{\log e}$ , so

$y = \frac{\left ( x ^{\log e} \right) ^{2} -1}{2 x ^{\log e}}= \frac{ x ^{2 \log e} -1}{2 x ^{\log e}}$

This makes the Cartesian equation

$y = \frac{ x ^{2 \log e} -1}{2 x ^{\log e}}$ .

Compare your answer with the correct one above

Question

Draw the graph of $r=sin\theta$ from $0\leq \theta \leq2\pi$ .

Answer

Between and $\frac{\pi }{2}$ , the radius approaches from .

From $\frac{\pi }{2}$ to $\pi$ the radius goes from to .

Between $\pi$ and $\frac{3\pi }{2}$ , the curve is redrawn in the opposite quadrant, the first quadrant as the radius approaches .

From $\frac{3\pi }{2}$ and $2\pi$ , the curve is redrawn in the second quadrant as the radius approaches from .

Compare your answer with the correct one above

Question

Draw the graph of $r=sin(2\theta )$ where $0\leq \theta \leq2\pi$ .

Answer

Because this function has a period of $\pi$ , the amplitude of the graph appear at a reference angle of $\frac{\pi }{4}$ (angles halfway between the angles of the axes).

Between and $\frac{\pi }{4}$ the radius approaches 1 from 0.

Between $\frac{\pi }{4}$ and $\frac{\pi }{2}$ , the radius approaches 0 from 1.

From $\frac{\pi }{2}$ to $\frac{3\pi }{4}$ the radius approaches -1 from 0 and is drawn in the opposite quadrant, the fourth quadrant because it has a negative radius.

Between $\frac{3\pi }{4}$ and $\pi$ , the radius approaches 0 from -1, and is also drawn in the fourth quadrant.

From $\pi$ and $\frac{5\pi }{4}$ , the radius approaches 1 from 0. Between $\frac{5\pi }{4}$ and $\frac{3\pi }{2}$ , the radius approaches 0 from 1.

Then between $\frac{3\pi }{2}$ and $\frac{7\pi }{4}$ the radius approaches -1 from 0. Because it is a negative radius, it is drawn in the opposite quadrant, the second quadrant. Likewise, as the radius approaches 0 from -1. Between $\frac{7\pi }{4}$ and $2\pi$ , the curve is drawn in the second quadrant.

Compare your answer with the correct one above

Question

Graph $r^2=cos(2\theta )$ where $0\leq \theta \leq2\pi$ .

Answer

Taking the graph of , we only want the areas in the positive first quadrant because the radius is squared and cannot be negative.

This leaves us with the areas from to $\frac{\pi }{4}$ , $\frac{3\pi }{4}$ to $\frac{5\pi }{4}$ , and $\frac{7\pi }{4}$ to $2\pi$ .

Then, when we take the square root of the radius, we get both a positive and negative answer with a maximum and minimum radius of $\pm 1$ .

To draw the graph, the radius is 1 at and traces to 0 at $\frac{\pi }{4}$ . As well, the negative part of the radius starts at -1 and traces to zero in the opposite quadrant, the third quadrant.

From $\frac{3\pi }{4}$ to $\pi$ , the curves are traced from 0 to 1 and 0 to -1 in the fourth quadrant. Following this pattern, the graph is redrawn again from the areas included in $\pi$ to $2\pi$ .

Compare your answer with the correct one above

Question

Draw the curve of $r^2=sin(2\theta )$ from $0\leq \theta \leq2\pi$ .

Answer

Taking the graph of , we only want the areas in the positive first quadrant because the radius is squared and cannot be negative.

This leaves us with the areas from to $\frac{\pi }{2}$ and $\pi$ to $\frac{3\pi }{2}$ .

Then, when we take the square root of the radius, we get both a positive and negative answer with a maximum and minimum radius of $\pm 1$ .

To draw the graph, the radius is 0 at and traces to 1 at $\frac{\pi }{4}$ . As well, the negative part of the radius starts at 0 and traces to-1 in the opposite quadrant, the third quadrant.

From $\frac{\pi }4{}$ to $\frac{\pi }{2}$ , the curves are traced from 1 to 0 and -1 to 0 in the third quadrant.

Following this pattern, the graph is redrawn again from the areas included in $\pi$ to $2\pi$ .

Compare your answer with the correct one above

Question

If and , what is in terms of (rectangular form)?

Answer

Given and , we can find in terms of by isolating in both equations:

$x=3+t\rightarrow t=x-3$

$y=4t+7\rightarrow t=\frac{y-7}{4}$

Since both of these transformations equal , we can set them equal to each other:

$\frac{y-7}{4}=x-3$

Compare your answer with the correct one above

Question

Find the length of the following parametric curve

$x=e^{t}cos(t)$ , $y=e^{t}sin(t)$ , $0\leq t \leq 2 \pi$ .

Answer

The length of a curve is found using the equation $L=\int_{\alpha }^{\beta }\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}dt$

We use the product rule,

$\frac{d}{dt}(ab)=a\frac{db}{dt}+b\frac{da}{dt}$ , when and are functions of ,

the trigonometric rule,

$\frac{d}{dt}[cos(t)]=-sin(t)$ and $\frac{d}{dt}[sin(t)]=cos(t)$

and exponential rule,

$\frac{d}{dt}[e^{t}]=e^{t}$ to find $\frac{dx}{dt}$ and $\frac{dy}{dt}$ .

In this case

$x=e^{t}cos(t)$ , $y=e^{t}sin(t)$

$\frac{dx}{dt}=\frac{d}{dt}e^{t}cos(t)=e^{t}\frac{d}{dt}cos(t)+cos(t)\frac{d}{dt}e^{t}$

$=e^{t}(-sin(t))+cos(t)e^{t}=e^{t}cos(t)-e^{t}sin(t)$

$\frac{dy}{dt}=\frac{d}{dt}e^{t}sin(t)=e^{t}\frac{d}{dt}sin(t)+sin(t)\frac{d}{dt}e^{t}$

$=e^{t}cos(t)+sin(t)e^{t}=e^{t}cos(t)+e^{t}sin(t)$

$\alpha=0, \beta=2\pi$

The length of this curve is

$L=\int_{0}^{2\pi }\sqrt{\left (e^{t}cos(t)-e^{t}sin(t)\right )^{2}+\left (e^{t}cos(t)+e^{t}sin(t)\right )^{2}}dt$

Using the identity $(a\pm b)^{2}=a^{2}\pm2ab+b^{2}$

$L=\int_{0}^{2\pi }\sqrt{\binom{\left (e^{2t}cos^{2}(t)-2e^{t}cos(t)e^{t}sin(t)+e^{2t}sin^{2}(t)\right )}{\left +(e^{2t}cos^{2}(t)+2e^{t}cos(t)e^{t}sin(t)+e^{2t}sin^{2}(t)\right)}dt}$

$=\int_{0}^{2\pi }\sqrt{(2e^{2t}cos^{2}(t)+2e^{2t}sin^{2}(t))dt}$

$=\int_{0}^{2\pi }\sqrt{2e^{2t}(cos^{2}(t)+sin^{2}(t))dt}$

Using the identity $\sqrt{a*b}=\sqrt{a}\sqrt{b}$

$L=\int_{0}^{2\pi }\sqrt{2e^{2t}} \sqrt{cos^{2}(t)+sin^{2}(t)dt}$

Using the trigonometric identity $sin^{2}(at)+cos^{2}(at)=1$ where is a constant and $e^{2t}=(e^{t})^2$

$=\int_{0}^{2\pi }\sqrt{2}e^{t}dt}=\sqrt{2}\int_{0}^{2\pi }e^{t}dt}$

Using the exponential rule, $\int e^{t}dt}=e^{t}$

$\sqrt{2}\int_{0}^{2\pi }e^{t}dt}=\sqrt{2}e^{t}|_{0}^{2\pi}=\sqrt{2}\left ( e^{2 \pi}-e^{0}}\right )$

Using the exponential rule, $e^{0}=1$ , gives us the final solution

$L=\sqrt{2}\left ( e^{2 \pi}-1}\right )$

Compare your answer with the correct one above

Question

Given and , what is the arc length between $0\leqt\leq t\leq4$ ?

Answer

In order to find the arc length, we must use the arc length formula for parametric curves:

$L=\int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}dt$ .

Given and , we can use using the Power Rule

$\frac{d}{dx}x^{n}=nx^{n-1}$ for all $n\neq0$ , to derive

$\frac{dx}{dt}=(1)t^{1-1}+(0)10=1$ and

$\frac{dy}{dt}=(1)2t^{1-1}-(0)9=2$ .

Plugging these values and our boundary values for into the arc length equation, we get:

$L=\int_{0}^{4}\sqrt{(1)^{2}+(2)^{2}}dt$

$L=\int_{0}^{4}(\sqrt{1+4})dt$

$L=\int_{0}^{4}(\sqrt{5})dt$

Now, using the Power Rule for Integrals

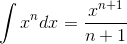$\int x^{n}dx=\frac{x^{n+1}}{n+1}$ for all $n\neq0$ ,

we can determine that:

$L=[t\sqrt{5}]_{0}^{4}\textrm{}dt$

$L=(4)\sqrt{5}-(0)\sqrt{5}$

$L=4\sqrt{5}$

Compare your answer with the correct one above

Question

Given and , what is the length of the arc from $0\leq t\leq2$ ?

Answer

In order to find the arc length, we must use the arc length formula for parametric curves:

$L=\int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}dt$ .

Given and , we can use using the Power Rule

$\frac{d}{dx}x^{n}=nx^{n-1}$ for all $n\neq0$ , to derive

$\frac{dx}{dt}=(1)4t^{1-1}-(0)5=4$ and

$\frac{dy}{dt}=(1)6t^{1-1}+(0)2=6$ .

Plugging these values and our boundary values for into the arc length equation, we get:

$L=\int_{0}^{2}(\sqrt{(4)^{2}+(6)^{2}}dt$

$L=\int_{0}^{2}(\sqrt{16+36})dt$

$L=\int_{0}^{2}(\sqrt{52})dt$

$L=\int_{0}^{2}(\sqrt{4\times13})dt$

$L=\int_{0}^{2}(2\sqrt{13})dt$

Now, using the Power Rule for Integrals

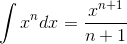$\int x^{n}dx=\frac{x^{n+1}}{n+1}$ for all $n\neq0$ ,

we can determine that:

$L=[2t\sqrt{13}]_{0}^{2}\textrm{}$

$L=2(2)\sqrt{13}-2(0)\sqrt{13}$

$L=4\sqrt{13}$

Compare your answer with the correct one above

Question

Find dy/dx at the point corresponding to the given value of the parameter without eliminating the parameter:

$x=5\sec(t),y=3\tan(t), t=\frac{\pi}{6}$

Answer

The formula for dy/dx for parametric equations is given as:

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$

From the problem statement:

$\frac{dy}{dt}=3\sec^2(t),\frac{dx}{dt}=5\sec(t)\tan(t)$

If we plug these into the above equation we end up with:

$\frac{dy}{dx}=\frac{3\sec^2(t)}{5\sec(t)\tan(t)}=\frac{3\sec(t)}{5\tan(t)}=\frac{3\frac{1}{cos(t)}}{5\frac{sin(t)}{cos(t)}}$

$\frac{dy}{dx}=\frac{3}{5}\frac{1}{\cos(t)}\frac{\cos(t)}{\sin(t)}=\frac{3}{5}\frac{1}{\sin(t)}$

If we plug in our given value for t, we end up with:

$\frac{3}{5}\frac{1}{\sin(\frac{\pi}{6})}=\frac{3}{5}\frac{1}{\frac{1}{2}}=\frac{3}{5}*2=\frac{6}{5}$

This is one of the answer choices.

Compare your answer with the correct one above

Question

Rewrite in polar form:

$x^{2} = 3xy + 1$

Answer

$x^{2} = 3xy + 1$

$\left (r \cos \theta \right ) ^{2} = 3\left (r \cos \theta \right )\left (r \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta = 3 r^{2} \cos \theta; \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta - 3 r^{2} \cos \theta; \sin \theta \right ) = 1$

$r ^{2} \left ( \ \cos ^{2} \theta - 3 \cos \theta; \sin \theta \right ) = 1$

$r ^{2} = \frac{1}{\cos ^{2} \theta - 3 \cos \theta; \sin \theta }$

$r =\sqrt{ \frac{1}{\cos ^{2} \theta - 3 \cos \theta; \sin \theta }}$

Compare your answer with the correct one above

Question

Graph the equation $r=cos(\theta )$ where $0\leq \theta \leq2\pi$ .

Answer

At angle the graph as a radius of . As it approaches $\frac{\pi }{2}$ , the radius approaches .

As the graph approaches $\pi$ , the radius approaches .

Because this is a negative radius, the curve is drawn in the opposite quadrant between $\frac{3\pi }{2}$ and $2\pi$ .

Between $\pi$ and $\frac{3\pi }{2}$ , the radius approaches from and redraws the curve in the first quadrant.

Between $\frac{3\pi }{2}$ and $2\pi$ , the graph redraws the curve in the fourth quadrant as the radius approaches from .

Compare your answer with the correct one above

Question

Draw the graph of $r=cos(2\theta )$ from $0\leq \theta \leq2\pi$ .

Answer

Because this function has a period of $\pi$ , the x-intercepts of the graph happen at a reference angle of $\frac{\pi }{4}$ (angles halfway between the angles of the axes).

Between and $\frac{\pi }{4}$ the radius approaches from .

Between $\frac{\pi }{4}$ and $\frac{\pi }{2}$ , the radius approaches from and is drawn in the opposite quadrant, the third quadrant because it has a negative radius.

From $\frac{\pi }{2}$ to $\frac{3\pi }{4}$ the radius approaches from , and is drawn in the fourth quadrant, the opposite quadrant.

Between $\frac{3\pi }{4}$ and $\pi$ , the radius approaches from .

From $\pi$ and $\frac{5\pi }{4}$ , the radius approaches from .

Between $\frac{5\pi }{4}$ and $\frac{3\pi }{2}$ , the radius approaches from . Because it is a negative radius, it is drawn in the opposite quadrant, the first quadrant.

Then between $\frac{3\pi }{2}$ and $\frac{7\pi }{4}$ the radius approaches from and is draw in the second quadrant.

Finally between $\frac{7\pi }{4}$ and $2\pi$ , the radius approaches from .

Compare your answer with the correct one above

Question

What is the following coordinate in polar form?

Provide the angle in degrees.

Answer

To calculate the polar coordinate, use

$r=\sqrt{x^2+y^2}$

$r=\sqrt{29}$

$\theta=tan^{-1}\left(\frac{y}{x}\right)=68$

However, keep track of the angle here. 68 degree is the mathematical equivalent of the expression, but we know the point (-2,-5) is in the 3rd quadrant, so we have to add 180 to it to get 248.

Some calculators might already have provided you with the correct answer.

$\theta=248$ .

Compare your answer with the correct one above

Question

What is the equation $y=2x^{2}$ in polar form?

Answer

We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given $y=2x^{2}$ , then $r\sin \theta=2(r\cos \theta )^{2}=2r^{2}\cos^{2} \theta$ .

$r\sin \theta=2(r\cos \theta )^{2}=2r^{2}\cos^{2} \theta$ . Dividing both sides by $r\cos \theta$ ,

$\tan \theta=2r\cos \theta$

$\frac{\tan \theta}{\cos \theta}=2r$

$\tan \theta}{\sec \theta=2r$

$\frac{1}{2}\tan \theta}{\sec \theta=r$

Compare your answer with the correct one above

Question

What is the equation $y=\frac{6}{x}$ in polar form?

Answer

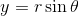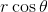We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given $y=\frac{6}{x}$ , then $r\sin \theta=\frac{6}{r\cos \theta}$ . Multiplying both sides by $r\cos \theta$ ,

$r^{2}\sin \theta cos \theta=6$

$r^{2}=\frac{6}{\sin \theta cos \theta}$

$r=\sqrt\frac{6}{\sin \theta cos \theta}$

Compare your answer with the correct one above

Question

Convert the following function into polar form:

Answer

The following formulas were used to convert the function from polar to Cartestian coordinates:

$x=r\cos(\theta), y=r\sin(\theta), x^2+y^2=r^2$

Note that the last formula is a manipulation of a trignometric identity.

Simply replace these with x and y in the original function.

$f(x)=2r^2+5rcos(\theta)+2$

Compare your answer with the correct one above

Question

What is the equation $y=-\frac{1}{2}x^{2}$ in polar form?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given $y=-\frac{1}{2}x^{2}$ , then:

$r\sin\theta=-\frac{1}{2}(r\cos \theta)^{2}$

$r\sin\theta=-\frac{1}{2}r^{2}\cos^{2} \theta$

Dividing both sides by $r\cos\theta$ , we get:

$\tan \theta=-\frac{1}{2}r\cos\theta$

$\frac{\tan \theta}{\cos\theta}=-\frac{1}{2}r$

$\tan \theta\sec\theta=-\frac{1}{2}r$

$r=-2\tan \theta\sec\theta$

Compare your answer with the correct one above

Question

What is the polar form of $y=-7x^{2}$ ?

Answer

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given $y=-7x^{2}$ , then:

$r\sin\theta=-7(r\cos\theta)^{2}$

$r\sin\theta=-7r^{2}\cos^{2}\theta$

Dividing both sides by $r\cos\theta$ , we get:

$\tan\theta=-7r\cos\theta$

$\frac{\tan\theta}{\cos\theta}=-7r$

$\tan\theta\sec\theta=-7r$

$r=-\frac{1}{7}\tan\theta\sec\theta$

Compare your answer with the correct one above

Tap the card to reveal the answer