Algebraic Functions - Algebra

Card 0 of 1620

Question

The monthly cost to insure your cars varies directly with the number of cars you own. Right now, you are paying \$420 per month to insure 3 cars, but you plan to get 2 more cars, so that you will own 5 cars. How much does it cost to insure 5 cars monthly?

Answer

The statement, 'The monthly costly to insure your cars varies directly with the number of cars you own' can be mathematically expressed as . M is the monthly cost, C is the number of cars owned, and k is the constant of variation.

Given that it costs \$420 a month to insure 3 cars, we can find the k-value.

Divide both sides by 3.

Now, we have the mathematical relationship.

Finding how much it costs to insure 5 cars can be found by substituting 5 for C and solving for M.

Compare your answer with the correct one above

Question

varies directly with the square root of . If , then . What is the value of if ?

Answer

If varies directly with the square root of , then for some constant of variation ,

$\small y = K \sqrt{x}$

If , then ; therefore, the equation becomes

$\small \small 48 = K \sqrt{25}$ ,

or

.

Divide by 5 to get , making the equation

$\small \small y = 9.6 \sqrt{x}$ .

If , then $\small \small \small y = 9.6 \sqrt{81} = 9.6 \cdot 9 = 86.4$ .

Compare your answer with the correct one above

Question

If an object is hung on a spring, the elongation of the spring varies directly as the mass of the object. A 20 kg object increases the length of a spring by exactly 7.2 cm. To the nearest tenth of a centimeter, by how much does a 32 kg object increase the length of the same spring?

Answer

Let be the mass of the weight and the elongation of the spring. Then for some constant of variation ,

We can find by setting from the first situation:

$7.2 = k \cdot 20$

$k = 7.2 \div 20 = 0.36$

so

In the second situation, we set and solve for :

$L = 0.36 \cdot32 =11.52$

which rounds to 11.5 centimeters.

Compare your answer with the correct one above

Question

If an object is hung on a spring, the elongation of the spring varies directly with the mass of the object. A 33 kilogram object increases the length of a spring by exactly 6.6 centimeters. To the nearest tenth of a kilogram, how much mass must an object posess to increase the length of that same spring by exactly 10 centimeters?

Answer

Let be the mass of the weight and the elongation of the spring, respectively. Then for some constant of variation ,

.

We can find by setting :

$6.6 = k \cdot 33$

$k = 6.6 \div 33 = 0.2$

Therefore .

Set and solve for :

$M = 10 \div 0.2 = 50$ kilograms

Compare your answer with the correct one above

Question

The volume of a fixed mass of gas varies inversely as the atmospheric pressure, as measured in millibars, acting on it, and directly as the temperature, as measured in kelvins, acting on it.

A balloon is filled to a capacity of exactly 100 cubic meters at a time at which the temperature is 310 kelvins and the atmospheric pressure is 1,020 millibars. The balloon is released, and an hour later, the balloon is subject to a pressure of 900 millibars and a temperature of 290 kelvins. To the nearest cubic meter, what is the new volume of the balloon?

Answer

If are the volume, pressure, and temperature, then the variation equation will be, for some constant of variation ,

$V = \frac{KT}{P}$

To calculate , substitute :

$100 = \frac{K \cdot 310}{1,020}$

$\frac{K \cdot 310}{1,020} \cdot \frac{1,020}{310} = 100 \cdot \frac{1,020}{310}$

The variation equation is

$V = \frac{329.03 T}{P}$

so substitute and solve for .

$V = \frac{329.03 \cdot 290}{900} \approx 106 \textrm{ m}^{3}$

Compare your answer with the correct one above

Question

If is directly proportional to and when at , what is the value of the constant of proportionality?

Answer

The general formula for direct proportionality is

where is the proportionality constant. To find the value of this , we plug in and

Solve for by dividing both sides by 12

$\frac{24}{12}=\frac{12k}{12}$

So .

Compare your answer with the correct one above

Question

The amount of money you earn is directly proportional to the nunber of hours you worked. On the first day, you earned \$32 by working 4 hours. On the second day, how many hours do you need to work to earn \$48.

Answer

The general formula for direct proportionality is

where is how much money you earned, is the proportionality constant, and is the number of hours worked.

Before we can figure out how many hours you need to work to earn \$48, we need to find the value of . It is given that you earned \$32 by working 4 hours. Plug these values into the formula

Solve for by dividing both sides by 4.

$\frac{32}{4}=\frac{4k}{4}$

So . We can use this to find out the hours you need to work to earn \$48. With , we have

Plug in \$48.

Divide both sides by 8

$\frac{48}{8}=\frac{8h}{8}$

So you will need to work 6 hours to earn \$48.

Compare your answer with the correct one above

Question

Does the equation below represent a direct variation? If it does, find the constant of variation.

Answer

Direct Variation is a relationship that can be represented by a function in the form

, where $k \neq 0$

is the constant of variation for a direct variation. is the coefficient of .

$y = \frac{2}{7}x$

The equation is in the form , so the equation is a direct variation.

The constant of variation or is $\frac{2}{7}$

Therefore, the answer is,

Yes it is a direct variation, $y = \frac{2}{7}x,$ with a direct variation of $\frac{2}{7}$

Compare your answer with the correct one above

Question

Suppose and , and that is in direct proportion with . What is the value of proportionality?

Answer

The general formula for direct proportionality is

where is our constant of proportionality. From here we can plug in the relevant values for and to get

Solving for requires that we divide both sides of the equation by , yielding

Compare your answer with the correct one above

Question

The cost of a catering company varies directly with the number of people attending. If the cost is \$100 when 20 people attend the party, find the constant of variation.

Answer

Because the cost varies directly with the number of people attending, we have the equation

Where is the cost and is the number of people attending.

We solve for , the constant of variation, by plugging in and .

And by dividing by 20 on both sides

$\frac{100}{20}=\frac{k(20) }{20}$

Yields

Compare your answer with the correct one above

Question

The amount of money Billy earns is directly proportional to his hours worked. Suppose he earns $\$12$ every eight hours of work. What is the minimum hours Billy must work in order to exceed $\$100$ ? Round to the nearest integer.

Answer

Write the formula for direct proportionality.

Let:

$x=\textup{hours worked}$

$y= \textup{earnings}$

Substitute twelve dollars and eight hours into this equation to solve for .

$\$12=k(8)$

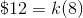
Divide by eight on both sides.

$k=\frac{12}{8} = \frac{3}{2}$

Substitute back into the formula.

$y=\frac{3}{2}x$

To find out the minimum number of hours Billy must work to make $\$100$ , substitute $\$100$ into and solve for .

$\$100=\frac{3}{2}x$

Multiply by two thirds on both sides.

$100\cdot \frac{2}{3}=\frac{3}{2}x \cdot \frac{2}{3}$

Simplify both sides.

$x=\frac{200}{3} = 66.\overline{6}$

Billy must work at least hours to earn as much required.

Compare your answer with the correct one above

Question

Given

$f\left ( x \right ) = 2x+3$

and

$g\left ( x \right ) = \frac{x-3}{2}$ .

Find $f\left ( g\left ( x \right ) \right )$ .

Answer

Starting with $f\left ( x \right ) = 2x+3$

Replace with $g\left ( x \right )$ .

We get the following:

$2\left ( \frac{x-3}{2} \right )+3=x-3+3$

Which is equal to .

Compare your answer with the correct one above

Question

Find the inverse of .

Answer

Interchange the x and y variables.

Subtract nine from both sides.

Simplify both sides.

Divide by two on both sides.

$\frac{x-9}{2}=\frac{2y}{2}$

Simplify the fractions.

$\frac{1}{2}x-\frac{9}{2}=y$

The inverse is: $y=\frac{1}{2}x-\frac{9}{2}$

Compare your answer with the correct one above

Question

Given:

and

$g(x)=\frac{x-3}{2}$ .

Find .

Answer

Start with which is equal to

$\frac{x-3}{2}$

and then replace with . We get the following:

$\frac{(2x+3)-3}{2}$

which is equal to

$\frac{2x}{2}=x$

Compare your answer with the correct one above

Question

Find the inverse of the following function:

$f(x) = x^{2}-3$

Answer

$f\left ( x \right ) = x^{2}-3$

which is the same as

$y = x^{2}-3$

If we solve for we get

$x^{2} = y +3$

Taking the square root of both sides gives us the following:

$x = \pm \sqrt{y+3}$

Interchanging and gives us

$y = \pm \sqrt{x + 3}$

Which is not one-to-one and therefore not a function.

Compare your answer with the correct one above

Question

The number of days to construct a house varies inversely with the number of people constructing that house. If it takes 28 days to construct a house with 6 people helping out, how long will it take if 20 people are helping out?

Answer

The statement, 'The number of days to construct a house varies inversely with the number of people constructing that house' has the mathematical relationship $D=\frac{k}{P}$ , where D is the number of days, P is the number of people, and k is the variation constant. Given that the house can be completed in 28 days with 6 people, the k-value is calculated.

$28=\frac{k}{6}$

This k-value can be used to find out how many days it takes to construct a house with 20 people (P = 20).

$D=\frac{168}{P}$

$D=\frac{168}{20}$

So it will take 8.4 days to build a house with 20 people.

Compare your answer with the correct one above

Question

varies directly with , and inversely with the square root of .

If and , then .

Find if and .

Answer

The variation equation can be written as below. Direct variation will put in the numerator, while inverse variation will put $\sqrt{z}$ in the denominator. is the constant that defines the variation.

$x=k* \frac{y}{\sqrt{z}}$

To find constant of variation, , substitute the values from the first scenario given in the question.

$10=k* \frac{6}{\sqrt{64}}=k* \frac{6}{8}=k* \frac{3}{4}$

$k=10\div\frac{3}{4}}= \frac{40}{3}$

We can plug this value into our variation equation.

$x=\frac{40}{3}\cdot \frac{y}{\sqrt{z}}$

Now we can solve for given the values in the second scenario of the question.

$x=\frac{40}{3}* \frac{9}{\sqrt{144}}=\frac{40}{3}* \frac{9}{12}=10$

Compare your answer with the correct one above

Question

is a one-to-one function specified in terms of a set of $\left ( x,y \right )$ coordinates:

A = $\left { \left ( 0,0 \right ), \left ( 1,2\right ),\left ( 2,4 \right ), \left ( 3,6 \right )\right }$

Which one of the following represents the inverse of the function specified by set A?

B = $\left { \left ( 0,0 \right ), \left ( 0,1 \right ), \left ( 0,2 \right ), \left ( 0,3 \right ) \right }$

C = $\left { \left ( 0,0 \right ), \left ( 2,1 \right ), \left ( 4,2 \right ), \left ( 6,3 \right ) \right }$

D = $\left { \left ( 1,1 \right ), \left ( 2,1 \right ), \left ( -2,1 \right ), \left ( 3,1 \right ) \right }$

E = $\left { \left ( -2,1 \right ), \left ( -2,5 \right ), \left ( -2,3 \right ), \left ( -2, -2 \right ) \right }$

F = $\left { \left ( 2,0 \right ), \left ( 2,-3 \right ),\left ( 2,5 \right ), \left ( 2,-7 \right ) \right }$

Answer

The set A is an one-to-one function of the form

One can find $f^{-1}\left ( x \right )$ by interchanging the and coordinates in set A resulting in set C.

Compare your answer with the correct one above

Question

$f(x) = x^{3} -5$

Which one of the following functions represents the inverse of $f\left ( x \right )?$

A)

B) $\sqrt[3]{x^{3}-5}$

C) $\sqrt[3]{x+5}$

D) $x^{3 } + 5$

E) $x^{3} - 5$

Answer

Given $y = x^{3} - 5$

Hence $x^{3}=y+5$

Interchanging with we get:

$y^{3}=x+5$

Solving for results in $y=\sqrt[3]{x+5}$ .

Compare your answer with the correct one above

Question

Find the inverse of:

Answer

Interchange the x and y variables.

Solve for y. First distribute the two inside the parentheses.

Subtract six from both sides.

Simplify.

Divide by two on both sides.

$\frac{x-6}{2}=\frac{2y}{2}$

Simplify and reduce.

The answer is: $y=\frac{1}{2}x -3$

Compare your answer with the correct one above

Tap the card to reveal the answer