How to find the length of the side of of an acute / obtuse isosceles triangle - ACT Math
Card 0 of 36
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


The answer is  .
.
Since we know that the permieter is 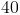 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 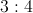 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 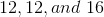 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 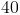


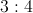





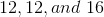

Compare your answer with the correct one above
In the standard  coordinate plane, the points
coordinate plane, the points  and
and  form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose  coordinate is between
coordinate is between  and
and  . If a vertex is placed at
. If a vertex is placed at  , the distance from
, the distance from  to this point will be
to this point will be  . The distance from
. The distance from  to this point will be the same.
to this point will be the same.
To form an isosceles triangle here, we need to create a third vertex whose 






Compare your answer with the correct one above

Note: Figure is not drawn to scale.
In the figure above, points  are collinear and
are collinear and 
 is a right angle. If
is a right angle. If  and
and 
 is
is  , what is
, what is  ?
?

Note: Figure is not drawn to scale.
In the figure above, points 






Because  is isosceles,
is isosceles,  equals
equals  or
or  .
.
We know that  add up to
add up to  , so
, so  must equal
must equal  or
or  .
.
Because 



We know that 




Compare your answer with the correct one above
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a  angle. The split beams each travel exactly
angle. The split beams each travel exactly  from the prism before striking two optic sensors (one for each beam).
from the prism before striking two optic sensors (one for each beam).
What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of  feet apiece, which meets the requirement for isosceles triangles, and having one angle of
feet apiece, which meets the requirement for isosceles triangles, and having one angle of  at the vertex where the two congruent sides meet means the other two angles must be
at the vertex where the two congruent sides meet means the other two angles must be  and
and  . The missing side connecting the two sensors, therefore, is opposite the
. The missing side connecting the two sensors, therefore, is opposite the  angle.
angle.
Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles  and
and  and opposite sides
and opposite sides  and
and  :
:
 .
.
Plugging in one of our  angles (and its corresponding
angles (and its corresponding  ft side) into this equation, as well as our
ft side) into this equation, as well as our  angle (and its corresponding unknown side) into this equation gives us:
angle (and its corresponding unknown side) into this equation gives us:

Next, cross-multiply:
 --->
---> 
Now simplify and solve:

Rounding, we see our missing side is  long.
long.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Compare your answer with the correct one above
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


The answer is  .
.
Since we know that the permieter is 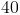 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 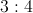 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 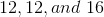 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 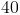


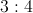





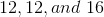

Compare your answer with the correct one above
In the standard  coordinate plane, the points
coordinate plane, the points  and
and  form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose  coordinate is between
coordinate is between  and
and  . If a vertex is placed at
. If a vertex is placed at  , the distance from
, the distance from  to this point will be
to this point will be  . The distance from
. The distance from  to this point will be the same.
to this point will be the same.
To form an isosceles triangle here, we need to create a third vertex whose 






Compare your answer with the correct one above

Note: Figure is not drawn to scale.
In the figure above, points  are collinear and
are collinear and 
 is a right angle. If
is a right angle. If  and
and 
 is
is  , what is
, what is  ?
?

Note: Figure is not drawn to scale.
In the figure above, points 






Because  is isosceles,
is isosceles,  equals
equals  or
or  .
.
We know that  add up to
add up to  , so
, so  must equal
must equal  or
or  .
.
Because 



We know that 




Compare your answer with the correct one above
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a  angle. The split beams each travel exactly
angle. The split beams each travel exactly  from the prism before striking two optic sensors (one for each beam).
from the prism before striking two optic sensors (one for each beam).
What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of  feet apiece, which meets the requirement for isosceles triangles, and having one angle of
feet apiece, which meets the requirement for isosceles triangles, and having one angle of  at the vertex where the two congruent sides meet means the other two angles must be
at the vertex where the two congruent sides meet means the other two angles must be  and
and  . The missing side connecting the two sensors, therefore, is opposite the
. The missing side connecting the two sensors, therefore, is opposite the  angle.
angle.
Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles  and
and  and opposite sides
and opposite sides  and
and  :
:
 .
.
Plugging in one of our  angles (and its corresponding
angles (and its corresponding  ft side) into this equation, as well as our
ft side) into this equation, as well as our  angle (and its corresponding unknown side) into this equation gives us:
angle (and its corresponding unknown side) into this equation gives us:

Next, cross-multiply:
 --->
---> 
Now simplify and solve:

Rounding, we see our missing side is  long.
long.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Compare your answer with the correct one above
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


The answer is  .
.
Since we know that the permieter is 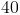 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 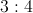 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 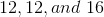 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 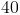


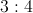





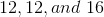

Compare your answer with the correct one above
In the standard  coordinate plane, the points
coordinate plane, the points  and
and  form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose  coordinate is between
coordinate is between  and
and  . If a vertex is placed at
. If a vertex is placed at  , the distance from
, the distance from  to this point will be
to this point will be  . The distance from
. The distance from  to this point will be the same.
to this point will be the same.
To form an isosceles triangle here, we need to create a third vertex whose 






Compare your answer with the correct one above

Note: Figure is not drawn to scale.
In the figure above, points  are collinear and
are collinear and 
 is a right angle. If
is a right angle. If  and
and 
 is
is  , what is
, what is  ?
?

Note: Figure is not drawn to scale.
In the figure above, points 






Because  is isosceles,
is isosceles,  equals
equals  or
or  .
.
We know that  add up to
add up to  , so
, so  must equal
must equal  or
or  .
.
Because 



We know that 




Compare your answer with the correct one above
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a  angle. The split beams each travel exactly
angle. The split beams each travel exactly  from the prism before striking two optic sensors (one for each beam).
from the prism before striking two optic sensors (one for each beam).
What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of  feet apiece, which meets the requirement for isosceles triangles, and having one angle of
feet apiece, which meets the requirement for isosceles triangles, and having one angle of  at the vertex where the two congruent sides meet means the other two angles must be
at the vertex where the two congruent sides meet means the other two angles must be  and
and  . The missing side connecting the two sensors, therefore, is opposite the
. The missing side connecting the two sensors, therefore, is opposite the  angle.
angle.
Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles  and
and  and opposite sides
and opposite sides  and
and  :
:
 .
.
Plugging in one of our  angles (and its corresponding
angles (and its corresponding  ft side) into this equation, as well as our
ft side) into this equation, as well as our  angle (and its corresponding unknown side) into this equation gives us:
angle (and its corresponding unknown side) into this equation gives us:

Next, cross-multiply:
 --->
---> 
Now simplify and solve:

Rounding, we see our missing side is  long.
long.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Compare your answer with the correct one above
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


The answer is  .
.
Since we know that the permieter is 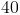 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 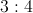 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 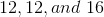 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 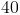


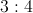





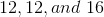

Compare your answer with the correct one above
In the standard  coordinate plane, the points
coordinate plane, the points  and
and  form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose  coordinate is between
coordinate is between  and
and  . If a vertex is placed at
. If a vertex is placed at  , the distance from
, the distance from  to this point will be
to this point will be  . The distance from
. The distance from  to this point will be the same.
to this point will be the same.
To form an isosceles triangle here, we need to create a third vertex whose 






Compare your answer with the correct one above

Note: Figure is not drawn to scale.
In the figure above, points  are collinear and
are collinear and 
 is a right angle. If
is a right angle. If  and
and 
 is
is  , what is
, what is  ?
?

Note: Figure is not drawn to scale.
In the figure above, points 






Because  is isosceles,
is isosceles,  equals
equals  or
or  .
.
We know that  add up to
add up to  , so
, so  must equal
must equal  or
or  .
.
Because 



We know that 




Compare your answer with the correct one above
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a  angle. The split beams each travel exactly
angle. The split beams each travel exactly  from the prism before striking two optic sensors (one for each beam).
from the prism before striking two optic sensors (one for each beam).
What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of  feet apiece, which meets the requirement for isosceles triangles, and having one angle of
feet apiece, which meets the requirement for isosceles triangles, and having one angle of  at the vertex where the two congruent sides meet means the other two angles must be
at the vertex where the two congruent sides meet means the other two angles must be  and
and  . The missing side connecting the two sensors, therefore, is opposite the
. The missing side connecting the two sensors, therefore, is opposite the  angle.
angle.
Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles  and
and  and opposite sides
and opposite sides  and
and  :
:
 .
.
Plugging in one of our  angles (and its corresponding
angles (and its corresponding  ft side) into this equation, as well as our
ft side) into this equation, as well as our  angle (and its corresponding unknown side) into this equation gives us:
angle (and its corresponding unknown side) into this equation gives us:

Next, cross-multiply:
 --->
---> 
Now simplify and solve:

Rounding, we see our missing side is  long.
long.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Compare your answer with the correct one above
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


The answer is  .
.
Since we know that the permieter is 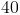 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 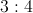 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 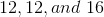 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 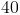


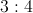





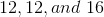

Compare your answer with the correct one above
In the standard  coordinate plane, the points
coordinate plane, the points  and
and  form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
form two vertices of an isosceles triangle. Which of the following points could be the third vertex?
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose  coordinate is between
coordinate is between  and
and  . If a vertex is placed at
. If a vertex is placed at  , the distance from
, the distance from  to this point will be
to this point will be  . The distance from
. The distance from  to this point will be the same.
to this point will be the same.
To form an isosceles triangle here, we need to create a third vertex whose 






Compare your answer with the correct one above

Note: Figure is not drawn to scale.
In the figure above, points  are collinear and
are collinear and 
 is a right angle. If
is a right angle. If  and
and 
 is
is  , what is
, what is  ?
?

Note: Figure is not drawn to scale.
In the figure above, points 






Because  is isosceles,
is isosceles,  equals
equals  or
or  .
.
We know that  add up to
add up to  , so
, so  must equal
must equal  or
or  .
.
Because 



We know that 




Compare your answer with the correct one above
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a  angle. The split beams each travel exactly
angle. The split beams each travel exactly  from the prism before striking two optic sensors (one for each beam).
from the prism before striking two optic sensors (one for each beam).
What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of  feet apiece, which meets the requirement for isosceles triangles, and having one angle of
feet apiece, which meets the requirement for isosceles triangles, and having one angle of  at the vertex where the two congruent sides meet means the other two angles must be
at the vertex where the two congruent sides meet means the other two angles must be  and
and  . The missing side connecting the two sensors, therefore, is opposite the
. The missing side connecting the two sensors, therefore, is opposite the  angle.
angle.
Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles  and
and  and opposite sides
and opposite sides  and
and  :
:
 .
.
Plugging in one of our  angles (and its corresponding
angles (and its corresponding  ft side) into this equation, as well as our
ft side) into this equation, as well as our  angle (and its corresponding unknown side) into this equation gives us:
angle (and its corresponding unknown side) into this equation gives us:

Next, cross-multiply:
 --->
---> 
Now simplify and solve:

Rounding, we see our missing side is  long.
long.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Compare your answer with the correct one above