How to find the angle of clock hands - ACT Math
Card 0 of 189
It is 4 o’clock. What is the measure of the angle formed between the hour hand and the minute hand?
It is 4 o’clock. What is the measure of the angle formed between the hour hand and the minute hand?
At four o’clock the minute hand is on the 12 and the hour hand is on the 4. The angle formed is 4/12 of the total number of degrees in a circle, 360.
4/12 * 360 = 120 degrees
At four o’clock the minute hand is on the 12 and the hour hand is on the 4. The angle formed is 4/12 of the total number of degrees in a circle, 360.
4/12 * 360 = 120 degrees
Compare your answer with the correct one above
Using the 8 hour analog clock from question 1 (an analog clock with 8 evenly spaced numbers on its face, with 8 where 12 normally is), what is the angle between the hands at 1:30? (Note: calculate the smaller angle, the one going between the hour and minute hand in a clockwise direction.)
Using the 8 hour analog clock from question 1 (an analog clock with 8 evenly spaced numbers on its face, with 8 where 12 normally is), what is the angle between the hands at 1:30? (Note: calculate the smaller angle, the one going between the hour and minute hand in a clockwise direction.)
Because it's an 8 hour clock, each section of the clock has an angle of 45 degrees due to the fact that 
.
When the clock reads 1:30 the hour hand is halfway in between the 1 and the 2, and the minute hand is on the 4 (at the bottom of the clock). Therefore, between the hour hand and the "2" on the clock there are 
degrees and between the 2 and the 4 there are 
degrees. Finally, 
Because it's an 8 hour clock, each section of the clock has an angle of 45 degrees due to the fact that
When the clock reads 1:30 the hour hand is halfway in between the 1 and the 2, and the minute hand is on the 4 (at the bottom of the clock). Therefore, between the hour hand and the "2" on the clock there are
Compare your answer with the correct one above
How many degrees are in each hour-long section of an analog clock with 8 equally spaced numbers on the face?
How many degrees are in each hour-long section of an analog clock with 8 equally spaced numbers on the face?
If creating a picture helps, draw a circle and place 8 at the top where 12 normally is. Then put 2, 4, and 6 at the positions of 3, 6, and 9 on a normal 12-hour analog clock. 1, 3, 5, and 7 go halfway in between each even number.
Now, because each section is equally spaced, and because there are 8 sections we simply divide the total number of degrees in a circle (
) by the number of sections (8). Thus:
If creating a picture helps, draw a circle and place 8 at the top where 12 normally is. Then put 2, 4, and 6 at the positions of 3, 6, and 9 on a normal 12-hour analog clock. 1, 3, 5, and 7 go halfway in between each even number.
Now, because each section is equally spaced, and because there are 8 sections we simply divide the total number of degrees in a circle (
Compare your answer with the correct one above
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
Compare your answer with the correct one above
What is the measure of the smaller angle formed by the hands of an analog watch if the hour hand is on the 10 and the minute hand is on the 2?
What is the measure of the smaller angle formed by the hands of an analog watch if the hour hand is on the 10 and the minute hand is on the 2?
A analog clock is divided up into 12 sectors, based on the numbers 1–12. One sector represents 30 degrees (360/12 = 30). If the hour hand is directly on the 10, and the minute hand is on the 2, that means there are 4 sectors of 30 degrees between then, thus they are 120 degrees apart (30 * 4 = 120).
A analog clock is divided up into 12 sectors, based on the numbers 1–12. One sector represents 30 degrees (360/12 = 30). If the hour hand is directly on the 10, and the minute hand is on the 2, that means there are 4 sectors of 30 degrees between then, thus they are 120 degrees apart (30 * 4 = 120).
Compare your answer with the correct one above
What is the angle between the hands of a standard 12-hour digital clock when it is 8:15? (note, give the smaller of the two angles, the one between the hands going clockwise
What is the angle between the hands of a standard 12-hour digital clock when it is 8:15? (note, give the smaller of the two angles, the one between the hands going clockwise
When the clock reads 8:15 the minute hand is on the 3 and the hour hand is just past the 8.
Each section of the clock is
degrees.
From 3 to 8 then there are 150 degrees. However, the hour hand has moved a quarter of the way between the 8 and the 9, or a quarter of 30 degrees. 
and so 
When the clock reads 8:15 the minute hand is on the 3 and the hour hand is just past the 8.
Each section of the clock is
From 3 to 8 then there are 150 degrees. However, the hour hand has moved a quarter of the way between the 8 and the 9, or a quarter of 30 degrees.
Compare your answer with the correct one above
What is the measure of the angle between the hands of a clock at 
? (compute the angle going clockwise from the hour hand to the minute hand)
What is the measure of the angle between the hands of a clock at
Each section of the clock is 
, and by 
the hour hand has gone three quarters of the way between the 
and the 
. Thus there are 
between the hour hand and the 
numeral. The minute hand is on the 
, and there are 
between the 
and the 
. So in total there are 
between the hands
Each section of the clock is
Compare your answer with the correct one above
On a 
analog clock (there is a 
where the 
normally is, a 
in the normal position of the 
, with 
where the 
is on a standard 
analog, the 
where the 
is on a standard analog, and 
and 
are at the spots normally occupied by 
and 
respectively), what is the angle between the hands when the clock reads 
?
On a
The number of degrees between each numeral on the clock face is equal to the number of degrees in a circle divided by the number of sections:
At 
the 
hand has gone 
way through the 
between the 
and the 
. Thus there are only 
left between it and the 3. There are 120 degrees between the 3 and the 5, where the minute hand is, so the total amount of degrees between the hands is:
The number of degrees between each numeral on the clock face is equal to the number of degrees in a circle divided by the number of sections:
At
Compare your answer with the correct one above
What is the angle between the clock hands when the clock reads 6:30?
What is the angle between the clock hands when the clock reads 6:30?
Remember there are 
in each hour long section of the clockface
.
When the clock reads 6:30 the minute hand is on the 6, and the hour hand is halfway between the 6 and 7.
Thus the number of degrees between the hands is
Remember there are
When the clock reads 6:30 the minute hand is on the 6, and the hour hand is halfway between the 6 and 7.
Thus the number of degrees between the hands is
Compare your answer with the correct one above
On a standard analog clock, what is the angle between the hands when the clock reads 
? Give the smaller of the two angles.
On a standard analog clock, what is the angle between the hands when the clock reads
To find the degrees of a clock hand, first find the angle between each hour-long sections. Since there are 
evenly spaced sections, we find that each section has an angle of: 
. at 
the hour hand has gone one-third of the way between the 
and 
. Thus there are two-thirds of 
between the hour hand and the 
. 
.
There are 
between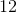 
and 
, where the minute hands is. Thus there's a total of 
between the hands.
To find the degrees of a clock hand, first find the angle between each hour-long sections. Since there are
There are
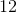
Compare your answer with the correct one above
On a 
analog clock (with a 
where the 
normally is and a 
where the 
normally is) what is the angle between the hands when the clock reads 
? (Give the smaller of the two angles)
On a
When the clock reads 
on this clock, the hour hand will be 
of the way between the 
and the 
. Since there are 
, evenly sized, sections of this clock each section has:
. And 
. At 
the minute hand will be one-quarter of the way around the entire dial. 
Thus the hands are 
from each other
When the clock reads
Thus the hands are
Compare your answer with the correct one above
A clock reads 
pm. What is the angle formed between the minute and hour hand on the clock?
A clock reads
When the clock reads 
, the hour hand is on the 
, and the minute hand is on the 
If we think about this as a fraction, there are twelve spots the hour hand can be on, which we means we are on the 
position.
Since there are 
in a circle, the angle can simply be found by multiplying this fraction by the number of degrees in a circle:
Alternatively, if the clock reads 
, the angle the clock reads is visually 
of the entire clock, which has 
.
.
When the clock reads
Since there are
Alternatively, if the clock reads
Compare your answer with the correct one above
What is the angle of the minor arc between the minute and hour hands of a clock reading 
? Assume a 
display (not a military clock).
What is the angle of the minor arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using 
as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains 
, and therefore for the minute hand, each minute past the hour takes up 
of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up 
of angular distance, which means each minute takes up 
of distance for the hour hand.
Thus, our distance from 
(our reference angle) in degrees for the minute hand can be expressed as 
, where 
is the number of minutes that have passed.
Likewise, our distance from 
in degrees for the hour hand can be expressed as 
, where 
is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, 
, and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are
Compare your answer with the correct one above
What is the angle of the minor arc between the minute and hour hands of a clock reading 
? Assume a 
display (not a military clock).
What is the angle of the minor arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using 
as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains 
, and therefore for the minute hand, each minute past the hour takes up 
of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up 
of angular distance, which means each minute takes up 
of distance for the hour hand.
Thus, our distance from 
(our reference angle) in degrees for the minute hand can be expressed as 
, where 
is the number of minutes that have passed.
Likewise, our distance from 
in degrees for the hour hand can be expressed as 
, where 
is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, 
, and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are
Compare your answer with the correct one above
What is the angle of the minor arc between the minute and hour hands of a clock reading 
? Assume a 
display (not a military clock).
What is the angle of the minor arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using 
as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains 
, and therefore for the minute hand, each minute past the hour takes up 
of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up 
of angular distance, which means each minute takes up 
of distance for the hour hand.
Thus, our distance from 
(our reference angle) in degrees for the minute hand can be expressed as 
, where 
is the number of minutes that have passed.
Likewise, our distance from 
in degrees for the hour hand can be expressed as 
, where 
is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, 
, and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are
Compare your answer with the correct one above
What is the angle of the major arc between the minute and hour hands of a clock reading 
? Assume a 
display (not a military clock).
What is the angle of the major arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using 
as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains , and therefore for the minute hand, each minute past the hour takes up of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up of angular distance, which means each minute takes up of distance for the hour hand.
Thus, our distance from (our reference angle) in degrees for the minute hand can be expressed as , where is the number of minutes that have passed.
Likewise, our distance from in degrees for the hour hand can be expressed as , where is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, , and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually 
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually
Thus, the hands are
Compare your answer with the correct one above
What is the angle of the major arc between the minute and hour hands of a clock reading 
? Assume a 
display (not a military clock).
What is the angle of the major arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using 
as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains , and therefore for the minute hand, each minute past the hour takes up of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up of angular distance, which means each minute takes up of distance for the hour hand.
Thus, our distance from (our reference angle) in degrees for the minute hand can be expressed as , where is the number of minutes that have passed.
Likewise, our distance from in degrees for the hour hand can be expressed as , where is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, , and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are
Compare your answer with the correct one above
What is the angle of the major arc between the minute and hour hands of a clock reading 
? Assume ab
display (not a military clock).
What is the angle of the major arc between the minute and hour hands of a clock reading
To find angular distance between the minute and hour hand, first find the position of each. Using as a reference (both hands straight up), we can calculate the difference in degree more easily.
First, remember that a circle contains , and therefore for the minute hand, each minute past the hour takes up of angular distance.
For the hour hand, each hour in a 12-hour cycle takes up of angular distance, which means each minute takes up of distance for the hour hand.
Thus, our distance from (our reference angle) in degrees for the minute hand can be expressed as , where is the number of minutes that have passed.
Likewise, our distance from in degrees for the hour hand can be expressed as , where is again the number of minutes that have passed.
Then, all we need to do is find the positive difference between these two measurements, , and we have our angle.
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually 
Thus, the hands are 
apart at 
.
To find angular distance between the minute and hour hand, first find the position of each. Using
First, remember that a circle contains
For the hour hand, each hour in a 12-hour cycle takes up
Thus, our distance from
Likewise, our distance from
Then, all we need to do is find the positive difference between these two measurements,
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually
Thus, the hands are
Compare your answer with the correct one above
A watch's hands move from 
to 
. What total angular distance does the minute hand move?
A watch's hands move from
First, remember that a circle contains , and therefore for the minute hand, each minute past the hour takes up of angular distance.
Thus, our total distance from our reference angle can be found as 
, where 
is the number of minutes that have elapsed.
In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved 
in total.
First, remember that a circle contains
Thus, our total distance from our reference angle can be found as
In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved
Compare your answer with the correct one above
A watch's hands move from 
to 
. What total angular distance does the minute hand move?
A watch's hands move from
First, remember that a circle contains , and therefore for the minute hand, each minute past the hour takes up of angular distance.
Thus, our total distance from our reference angle can be found as 
, where 
is the number of minutes that have elapsed.
In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved 
in total.
First, remember that a circle contains
Thus, our total distance from our reference angle can be found as
In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved
Compare your answer with the correct one above