Introduction - Abstract Algebra
Card 0 of 8
Which of the following is an identity element of the binary operation  ?
?
Which of the following is an identity element of the binary operation 
Tap to see back →
Defining the binary operation  will help in understanding the identity element. Say
will help in understanding the identity element. Say 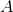 is a set and the binary operator is defined as
is a set and the binary operator is defined as  for all given pairs in
for all given pairs in  .
.
Then there exists an identity element  in
in  such that given,
such that given,

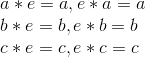
Therefore, looking at the possible answer selections the correct answer is,

Defining the binary operation 
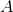


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following illustrates the inverse element?
Which of the following illustrates the inverse element?
Tap to see back →
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every  such that
such that  where
where  and
and  is an identity element.
is an identity element.
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 



Which of the following is an identity element of the binary operation  ?
?
Which of the following is an identity element of the binary operation 
Tap to see back →
Defining the binary operation  will help in understanding the identity element. Say
will help in understanding the identity element. Say 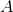 is a set and the binary operator is defined as
is a set and the binary operator is defined as  for all given pairs in
for all given pairs in  .
.
Then there exists an identity element  in
in  such that given,
such that given,

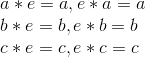
Therefore, looking at the possible answer selections the correct answer is,

Defining the binary operation 


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following illustrates the inverse element?
Which of the following illustrates the inverse element?
Tap to see back →
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every  such that
such that  where
where  and
and  is an identity element.
is an identity element.
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 



Which of the following is an identity element of the binary operation  ?
?
Which of the following is an identity element of the binary operation 
Tap to see back →
Defining the binary operation  will help in understanding the identity element. Say
will help in understanding the identity element. Say  is a set and the binary operator is defined as
is a set and the binary operator is defined as  for all given pairs in
for all given pairs in  .
.
Then there exists an identity element  in
in  such that given,
such that given,

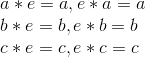
Therefore, looking at the possible answer selections the correct answer is,

Defining the binary operation 
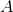


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following illustrates the inverse element?
Which of the following illustrates the inverse element?
Tap to see back →
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every  such that
such that  where
where  and
and  is an identity element.
is an identity element.
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 



Which of the following is an identity element of the binary operation  ?
?
Which of the following is an identity element of the binary operation 
Tap to see back →
Defining the binary operation  will help in understanding the identity element. Say
will help in understanding the identity element. Say 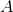 is a set and the binary operator is defined as
is a set and the binary operator is defined as  for all given pairs in
for all given pairs in  .
.
Then there exists an identity element  in
in  such that given,
such that given,

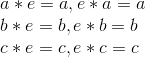
Therefore, looking at the possible answer selections the correct answer is,

Defining the binary operation 
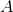


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Which of the following illustrates the inverse element?
Which of the following illustrates the inverse element?
Tap to see back →
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every  such that
such that  where
where  and
and  is an identity element.
is an identity element.
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 


