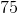Use Measure of Center and Measure of Variability to Compare Populations: CCSS.Math.Content.7.SP.B.4
Help Questions
7th Grade Math › Use Measure of Center and Measure of Variability to Compare Populations: CCSS.Math.Content.7.SP.B.4
Two businesses monitored their profits for a week. Which business made the most profit, and what was the average profit per day of that business?

Business A-
Business A-
Business B-
Business B-
Explanation
This is a two part problem. First, we need to find out which business made the most profit during the week. To do this, we simply add up the profits from each day:
Business A:
Business B:
Business B made the most profit, so the answer choices that said Business A made the most profit can be eliminated.
To solve for the mean, we can take our added profits and divide them by the number of addends, which is 
Business A:
Business B:
A teacher is comparing two students' median test scores, as shown in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student B-
Student A-
Student A-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
Two businesses monitored their profits for a week. Which business made the most profit, and what was the average profit per day of that business?

Business B-
Business A-
Business B-
Business A-
Explanation
This is a two part problem. First, we need to find out which business made the most profit during the week. To do this, we simply add up the profits from each day:
Business A:
Business B:
Business B made the most profit, so the answer choices that said Business A made the most profit can be eliminated.
To solve for the mean, we can take our added profits and divide them by the number of addends, which is 
Business A:
Business B:
Two businesses monitored their profits for a week. Which business made the most profit, and what was the average profit per day of that business?

Business A-
Business A-
Business B-
Business B-
Explanation
This is a two part problem. First, we need to find out which business made the most profit during the week. To do this, we simply add up the profits from each day:
Business A:
Business B:
Business A made the most profit, so the answer choices that said Business B made the most profit can be eliminated.
To solve for the mean, we can take our added profits and divide them by the number of addends, which is 
Business A:
Business B:
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student B-
Student A-
Student A-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student A-
Student A-
Student B-
Student B-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student A has the higher median score,
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student A-
Student A-
Student B-
Student B-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student A has the higher median score,
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student A-
Student B-
Student B-
Student A-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student A has the higher median score,
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student B-
Student A-
Student A-
Explanation
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
Two businesses monitored their profits for a week. Which business made the most profit, and what was the average profit per day of that business?

Business B-
Business B-
Business A-
Business A-
Explanation
This is a two part problem. First, we need to find out which business made the most profit during the week. To do this, we simply add up the profits from each day:
Business A:
Business B:
Business B made the most profit, so the answer choices that said Business A made the most profit can be eliminated.
To solve for the mean, we can take our added profits and divide them by the number of addends, which is 
Business A:
Business B: