Solve Simple Equations for an Unknown Angle in a Figure: CCSS.Math.Content.7.G.B.5
Help Questions
7th Grade Math › Solve Simple Equations for an Unknown Angle in a Figure: CCSS.Math.Content.7.G.B.5
What angle is complement to 
Explanation
The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90. In this case, since we are given the angle in radians, we are subtracting from 
Reconvert the fractions to the least common denominator.
Reduce the fraction.
Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a triangle:
Now that we have the correct formula, we can substitute in our known values and solve:
The figure represents a set of complementary angles, solve for 

Explanation
Complementary angles are defined as two angles that when added together equal
From the question, we know that the two angles are complimentary, and thus equal 
Next we can solve for 
What is the supplementary angle to 
Explanation
Supplementary angles add up to 

One angle of an isosceles triangle has measure 
Not enough information is given to answer this question.
Explanation
An isosceles triangle not only has two sides of equal measure, it has two angles of equal measure. This means one of two things, which we examine separately:
Case 1: It has another 
Case 2: Its other two angles are the ones that are of equal measure. If we let 

Both angles measure
What angle is complementary to 
Explanation
To find the other angle, subtract the given angle from 

The complementary is:
The figure represents a set of supplementary angles, solve for 

Explanation
Supplementary angles are defined as two angles that when added together equal
From the question, we know that the two angles are supplementary, and thus equal 
Next we can solve for 
Solve for 

Explanation
A pair of intersecting angles is illustrated by the provided image.


Solve for 

Explanation
A pair of intersecting angles is illustrated by the provided image.


The figure represents a set of complementary angles, solve for 

Explanation
Complementary angles are defined as two angles that when added together equal
From the question, we know that the two angles are complimentary, and thus equal 
Next we can solve for 
























![\frac{\begin{array}[b]{r}x+25=90\ -25-25\end{array}}{x= 65}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/928303/gif.latex)


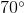



























![\frac{\begin{array}[b]{r}x+109=180\ -109-109\end{array}}{x= 71}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931843/gif.latex)


















![\frac{\begin{array}[b]{r}x+20=90\ -20-20\end{array}}{x= 70}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/928317/gif.latex)